题目内容
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,记
时,记![]() 的极大值为
的极大值为![]() ,极小值为
,极小值为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]()
【解析】【试题分析】(1)先对函数![]() 求导得到
求导得到![]() ,再对参数
,再对参数![]() 分两类进行讨论:
分两类进行讨论: ![]() 时,
时, ![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立, ![]() 在区间
在区间![]() 上单调递增;
上单调递增; ![]() 时,
时, ![]() 有两根,记
有两根,记![]() ,则
,则![]() ,由
,由![]() 得
得![]() ,解得
,解得![]() 或
或![]() ,所以递增区间是
,所以递增区间是![]() ,递减区间是
,递减区间是![]() ;(2)先借助(1)的结论求出
;(2)先借助(1)的结论求出![]() 进而转化为求
进而转化为求![]() 的值域,又
的值域,又![]() ,
,
所以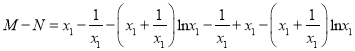
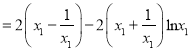 ,然后构造函数
,然后构造函数![]() ,求导可得
,求导可得![]() ,即
,即![]() ,所以当
,所以当![]() 时,
时, ![]() ,即
,即![]() 在
在![]() 时单调递减,由
时单调递减,由 ,当
,当![]() 时,
时, ![]() 递减,又
递减,又![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,所以
,所以![]() ,所以
,所以![]() ,最后求出
,最后求出![]() 的取值范围是
的取值范围是![]() .
.
解:(1)函数![]() 的定义域为
的定义域为![]() ,
, ![]() ,
,
(一)![]() 时,
时, ![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立, ![]() 在区间
在区间![]() 上单调递增;(二)
上单调递增;(二)![]() 时,
时, ![]() 有两根,记
有两根,记![]() ,则
,则![]() ,
,
由![]() 得
得![]() ,解得
,解得![]() 或
或![]() ,
,
所以递增区间是![]() ,递减区间是
,递减区间是![]() .
.
(2)当![]() 时,由(1)得
时,由(1)得![]() ,
,
所以![]() ,又
,又![]() ,
,
所以
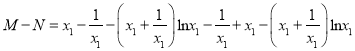
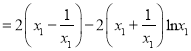 ,
,
记![]() ,则
,则![]() ,
,
即![]() ,所以当
,所以当![]() 时,
时, ![]() ,即
,即![]() 在
在![]() 时单调递减,
时单调递减,
由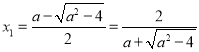 ,当
,当![]() 时,
时, ![]() 递减,
递减,
又![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某畜牧站为了考查某种新型药物预防动物疾病的效果,利用小白鼠进行试验,得到如下丢失数据的![]() 列联表
列联表
患病 | 未患病 | 总计 | |
没服用药 | 20 | 30 | 50 |
服用药 |
|
| 50 |
总计 |
|
| 100 |
设从没服用药的小白鼠中任取两只,未患病的动物数为![]() ,从服用药物的小白鼠中任取两只,未患病的动物数为
,从服用药物的小白鼠中任取两只,未患病的动物数为![]() ,得到如下比例关系:
,得到如下比例关系:![]()
(1)求出![]() 列联表中数据
列联表中数据![]() ,
,![]() ,
,![]() ,
,![]() 的值
的值
(2)是否有![]() 的把握认为药物有效?并说明理由
的把握认为药物有效?并说明理由
(参考公式:![]() ,当
,当![]() 时,有
时,有![]() 的把握认为A与B有关;
的把握认为A与B有关;![]() 时,有
时,有![]() 的把握认为A与B有关.
的把握认为A与B有关.