题目内容
【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜食 | 不喜欢甜食 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
附: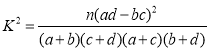
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
【答案】(1)有;(2)![]() .
.
【解析】
(1)将列联表中的数据代入公式可求得![]() ,再与3.841进行比较即可得解;
,再与3.841进行比较即可得解;
(2)由题意结合列举法求出所有的基本事件数及符合要求的基本事件数,再由古典概型概率公式即可得解.
(1)将列联表中的数据代入公式可得
![]() ,
,
所以有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)2名喜欢甜品的学生记为![]() ,3名不喜欢甜品学生记为
,3名不喜欢甜品学生记为![]() ,
,
则从这5名学生中随机抽取3人的基本事件为:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共10种;
,共10种;
3人中至多有1人喜欢甜品的基本事件为:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共7种;
,共7种;
所以至多有1人喜欢甜品的概率![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】对某校高三年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率统计表和频率分布直方图如下:
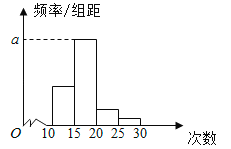
分组 | 频数 | 频率 |
| 15 | 0.30 |
| 29 |
|
|
|
|
| 2 |
|
合计 |
| 1 |
(1)求出表中![]() ,
,![]() 及图中
及图中![]() 的值;
的值;
(2)若该校高三学生人数有500人,试估计该校高三学生参加社区服务的次数在区间![]() 内的人数;
内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间![]() 内的概率.
内的概率.
