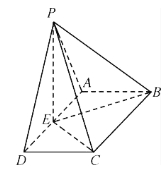
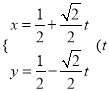题目内容
【题目】已知椭圆
经过点
，且其右焦点与抛物线
的焦点
重合.
（1）求椭圆
的方程；
（2）直线
经过点与椭圆相交于
、
两点，与抛物线
相交于
、
两点.求
的最大值.
【答案】（1）
（2）
【解析】
（1）根据抛物线方程得出椭圆的焦点坐标，结合椭圆经过的点，求解椭圆方程；
（2）联立直线与曲线方程，结合韦达定理处理弦长的比例关系即可得解.
（1）由抛物线方程为
，得其焦点
，
∵椭圆右焦点与抛物线焦点重合，
.
故
①
又椭圆
经过点
②
由①②消去
并整理，得，
，解得：
，或
（舍去），
从而
.故椭圆的方程为.
（2）当直线
垂直于
轴时，
则
.
当直线与轴不垂直，设其斜率为
，则直线的方程为：
.
联立
，得：
.
.
∴方程有两个不等的实数根.设
.
则
.
所以，
.
由
，得，
.
，∴方程有两个不等的实数根.设
.
，
由抛物线的定义，得
.
.
综上，当直线垂直于轴时，
取得最大值.
【题目】某企业通过调查问卷（满分50分）的形式对本企业900名员工的工作满意程度进行调查，并随机抽取了其中30名员工（16名女工，14名男工）的得分，如下表：
女 | 47 | 36 | 32 | 48 | 34 | 44 | 43 | 47 | 46 | 41 | 43 | 42 | 50 | 43 | 35 | 49 |
男 | 37 | 35 | 34 | 43 | 46 | 36 | 38 | 40 | 39 | 32 | 48 | 33 | 40 | 34 |
（1）根据以上数据，估计该企业得分大于45分的员工人数；
（2）现用计算器求得这30名员工的平均得分为40.5分，若规定大于平局得分为 “满意”，否则为 “不满意”，请完成下列表格：
“满意”的人数 | “不满意”的人数 | 合计 | |
女员工 | 16 | ||
男员工 | 14 | ||
合计 | 30 |
（3）根据上述表中数据，利用独立性检验的方法判断，能否在犯错误的概率不超过1%的前提下，认为该企业员工“性别”与“工作是否满意”有关？
参考数据：
P(K2 | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
K | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】某大学餐饮中心为了了解新生的饮食习惯，在全校一年级学生中进行了抽样调查，调查结果如下表所示：
喜欢甜食 | 不喜欢甜食 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
附：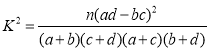
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
（1）根据表中数据，问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”；
（2）已知在被调查的北方学生中有5名数学系的学生，其中2名喜欢甜品，现在从这5名学生中随机抽取3人，求至多有1人喜欢甜品的概率.
【题目】为了研究一种昆虫的产卵数
和温度
是否有关，现收集了7组观测数据列于下表中，并作出了如图的散点图．
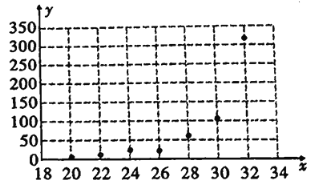
温度 | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
产卵数 | 6 | 10 | 22 | 26 | 64 | 118 | 310 |
|
|
|
|
|
|
|
26 | 79．4 | 3．58 | 112 | 11．6 | 2340 | 35．72 |
其中
．
（1）根据散点图判断，
与
哪一个更适宜作为该昆虫的产卵数与温度的回归方程类型？（给出判断即可，不必说明理由）．
（2）根据表中数据，建立关于的回归方程；（保留两位有效数字）
（3）根据关于的回归方程，估计温度为33℃时的产卵数．
（参考数据：
）
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘估计分别为
．
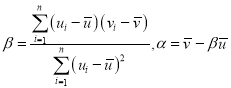【题目】某学校为了了解学生使用手机的情况，分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频数分布表和频率分布直方图，将使用手机时间不低于80分钟的学生称为“手机迷”.
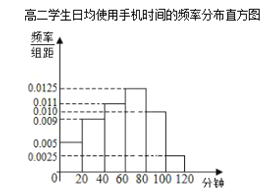
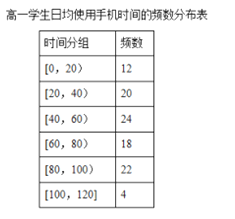
（I）将频率视为概率，估计哪个年级的学生是“手机迷”的概率大？请说明理由.
（II）在高二的抽查中，已知随机抽到的女生共有55名，其中10名为“手机迷”.根据已知条件完成下面的2×2列联表，并据此资料你有多大的把握认为“手机迷”与性别有关？
非手机迷 | 手机迷 | 合计 | |
男 | |||
女 | |||
合计 |
附：随机变量
（其中
为样本总量）.
参考数据 |
| 0.15 | 0.10 | 0.05 | 0.025 |
| span>2.072 | 2.706 | 3.841 | 5.024 |
