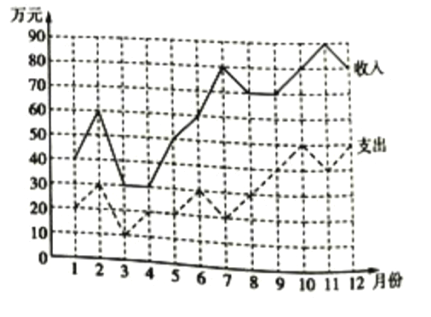
题目内容
【题目】定义首项为1且公比为正数的等比数列为“M-数列”.
(1)已知等比数列{an}满足:![]() ,求证:数列{an}为“M-数列”;
,求证:数列{an}为“M-数列”;
(2)已知数列{bn}满足:![]() ,其中Sn为数列{bn}的前n项和.
,其中Sn为数列{bn}的前n项和.
①求数列{bn}的通项公式;
②设m为正整数,若存在“M-数列”{cn}![]() ,对任意正整数k,当k≤m时,都有
,对任意正整数k,当k≤m时,都有![]() 成立,求m的最大值.
成立,求m的最大值.
【答案】(1)见解析;
(2)①bn=n![]() ;②5.
;②5.
【解析】
(1)由题意分别求得数列的首项和公比即可证得题中的结论;
(2)①由题意利用递推关系式讨论可得数列{bn}是等差数列,据此即可确定其通项公式;
②由①确定![]() 的值,将原问题进行等价转化,构造函数,结合导函数研究函数的性质即可求得m的最大值.
的值,将原问题进行等价转化,构造函数,结合导函数研究函数的性质即可求得m的最大值.
(1)设等比数列{an}的公比为q,所以a1≠0,q≠0.
由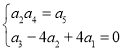 ,得
,得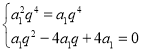 ,解得
,解得![]() .
.
因此数列![]() 为“M—数列”.
为“M—数列”.
(2)①因为![]() ,所以
,所以![]() .
.
由![]() 得
得![]() ,则
,则![]() .
.
由![]() ,得
,得![]() ,
,
当![]() 时,由
时,由![]() ,得
,得![]() ,
,
整理得![]() .
.
所以数列{bn}是首项和公差均为1的等差数列.
因此,数列{bn}的通项公式为bn=n![]() .
.
②由①知,bk=k,![]() .
.
因为数列{cn}为“M–数列”,设公比为q,所以c1=1,q>0.
因为ck≤bk≤ck+1,所以![]() ,其中k=1,2,3,…,m.
,其中k=1,2,3,…,m.
当k=1时,有q≥1;
当k=2,3,…,m时,有![]() .
.
设f(x)=![]() ,则
,则![]() .
.
令![]() ,得x=e.列表如下:
,得x=e.列表如下:
x |
| e | (e,+∞) |
| + | 0 | – |
|
| 极大值 |
|
因为![]() ,所以
,所以![]() .
.
取![]() ,当k=1,2,3,4,5时,
,当k=1,2,3,4,5时,![]() ,即
,即![]() ,
,
经检验知![]() 也成立.
也成立.
因此所求m的最大值不小于5.
若m≥6,分别取k=3,6,得3≤q3,且q5≤6,从而q15≥243,且q15≤216,
所以q不存在.因此所求m的最大值小于6.
综上,所求m的最大值为5.

 名校课堂系列答案
名校课堂系列答案【题目】在贯彻中共中央、国务院关于精准扶贫政策的过程中,某单位在某市定点帮扶某村![]() 户贫困户.为了做到精准帮扶,工作组对这
户贫困户.为了做到精准帮扶,工作组对这![]() 户村民的年收入情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标
户村民的年收入情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标![]() .将指标
.将指标![]() 按照
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成五组,得到如图所示的频率分布直方图.规定若
分成五组,得到如图所示的频率分布直方图.规定若![]() ,则认定该户为“绝对贫困户”,否则认定该户为“相对贫困户”;当
,则认定该户为“绝对贫困户”,否则认定该户为“相对贫困户”;当![]() 时,认定该户为“亟待帮住户”.工作组又对这
时,认定该户为“亟待帮住户”.工作组又对这![]() 户家庭的受教育水平进行评测,家庭受教育水平记为“良好”与“不好”两种.
户家庭的受教育水平进行评测,家庭受教育水平记为“良好”与“不好”两种.

(1)完成下面的列联表,并判断是否有![]() 的把握认为绝对贫困户数与受教育水平不好有关:
的把握认为绝对贫困户数与受教育水平不好有关:
受教育水平良好 | 受教育水平不好 | 总计 | |
绝对贫困户 |
| ||
相对贫困户 |
| ||
总计 |
|
(2)上级部门为了调查这个村的特困户分布情况,在贫困指标处于![]() 的贫困户中,随机选取两户,用
的贫困户中,随机选取两户,用![]() 表示所选两户中“亟待帮助户”的户数,求
表示所选两户中“亟待帮助户”的户数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
附: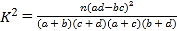 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|