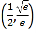题目内容
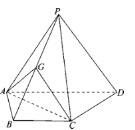
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点.
的中点.
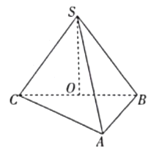
(1)求证:![]() 面
面![]() ;
;
(2)求二面角![]() 的平面角的正弦值.
的平面角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)利用等腰三角形的性质得到![]() ,由勾股定理逆定理得
,由勾股定理逆定理得![]() ,由线面垂直的判定定理即可证明;
,由线面垂直的判定定理即可证明;
(2)建立空间直角坐标系,分别求出面![]() 与面
与面![]() 的法向量,利用向量的夹角公式计算法向量夹角,从而可得二面角
的法向量,利用向量的夹角公式计算法向量夹角,从而可得二面角![]() 的平面角的正弦值.
的平面角的正弦值.
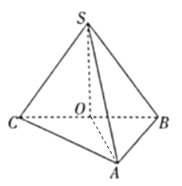
解:(1)连接![]() ,设
,设![]() ,则
,则![]() ,
,
![]()
![]() ,
,![]() 为
为![]() 的中点
的中点
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() 为
为![]() 的中点
的中点
![]()
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)由(1)知,![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,![]() 两两垂直,
两两垂直,
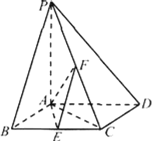
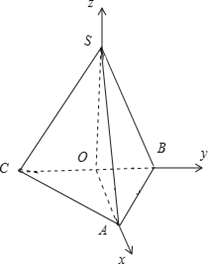
如图,以![]() 为原点,以
为原点,以![]() ,
,![]() ,
,![]() 所在射线为
所在射线为![]() ,
,![]() ,
,![]() 轴正半轴,建立空间直角坐标系,
轴正半轴,建立空间直角坐标系,
则![]() ,
,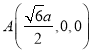 ,
,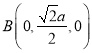 ,
,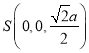 ,
,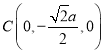 ,
,
∴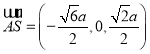 ,
,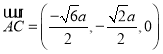 .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则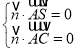 ,即
,即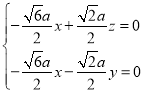 ,
,
![]()
![]() ,
,
取![]() ,则
,则![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]() 面
面![]() ,
,
![]() 可取向量
可取向量![]() 为平面
为平面![]() 的法向量,
的法向量,
![]()
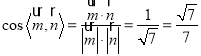 ,
,
![]() 二面角
二面角![]() 的平面角的正弦值为
的平面角的正弦值为![]() .
.

练习册系列答案
相关题目
【题目】某市正在进行创建全国文明城市的复验工作,为了解市民对“创建全国文明城市”的知识知晓程度,某权威调查机构对市民进行随机调查,并对调查结果进行统计,共分为优秀和一般两类,先从结果中随机抽取100份,统计得出如下![]() 列联表:
列联表:
优秀 | 一般 | 总计 | |
男 | 25 | 25 | 50 |
女 | 30 | 20 | 50 |
总计 | 55 | 45 | 100 |
(1)根据上述列联表,是否有![]() 的把握认为“创城知识的知晓程度是否为优秀与性别有关”?
的把握认为“创城知识的知晓程度是否为优秀与性别有关”?
(2)现从调查结果为一般的市民中,按分层抽样的方法从中抽取9人,然后再从这9人中随机抽取3人,求这三位市民中男女都有的概率;
(3)以样本估计总体,视样本频率为概率,从全市市民中随机抽取10人,用![]() 表示这10人中优秀的人数,求随机变量
表示这10人中优秀的人数,求随机变量![]() 的期望和方差.
的期望和方差.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
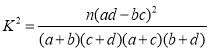 (其中
(其中![]() ).
).