题目内容
【题目】已知二次函数f(x)=x2+bx+c(b,c∈R)
(1)若f(x)的图象与x轴有且仅有一个交点,求b2+c2+2的取值范围;
(2)在b≥0的条件下,若f(x)的定义域[﹣1,0],值域也是[﹣1,0],符合上述要求的函数f(x)是否存在?若存在,求出f(x)的表达式,若不存在,请说明理由.
【答案】
(1)解:由于f(x)的图象与x轴有且仅有一个交点,故△=0,
即△=b2﹣4c=0b2=4c,
则b2+c2+2=c2+4c+2=(c+2)2﹣4≥﹣4;
(2)解:设符合条件的f(x)存在,
∵函数图象的对称轴是x=﹣ ![]() ,
,
又b≥0,∴﹣ ![]() ≤0.
≤0.
①当﹣ ![]() <﹣
<﹣ ![]() ≤0,即0≤b<1时,
≤0,即0≤b<1时,
函数x=﹣ ![]() 有最小值﹣1,则
有最小值﹣1,则 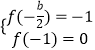
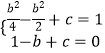
![]() 或
或 ![]() (舍去).
(舍去).
②当﹣1<﹣ ![]() ≤﹣
≤﹣ ![]() ,即1≤b<2时,则
,即1≤b<2时,则 
![]() (舍去)或
(舍去)或 ![]() (舍去).
(舍去).
③当﹣ ![]() ≤﹣1,即b≥2时,函数在[﹣1,0]上单调递增,则
≤﹣1,即b≥2时,函数在[﹣1,0]上单调递增,则 ![]() ,解得
,解得 ![]() ,
,
综上所述,符合条件的函数有两个,
f(x)=x2﹣1或f(x)=x2+2x
【解析】(1)根据二次函数的性质得到判别式△=0,求出b2=4c,代入b2+c2+2,求出其范围即可;(2)二次函数f(x)=x2+bx+c(b≥0,c∈R)的对称轴是x=﹣ ![]() ,定义域为[﹣1,0],按照对称轴在定义域[﹣1,0]内、在[﹣1,0]的左边和在[﹣1,0]的右边三种情况分别求函数的值域,令其和题目条件中给出的值域相等,求b和c.
,定义域为[﹣1,0],按照对称轴在定义域[﹣1,0]内、在[﹣1,0]的左边和在[﹣1,0]的右边三种情况分别求函数的值域,令其和题目条件中给出的值域相等,求b和c.
【考点精析】掌握二次函数的性质是解答本题的根本,需要知道当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.

练习册系列答案
相关题目