题目内容
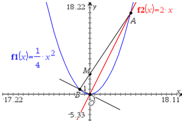
已知直线l:y=2x与抛物线C:y=
x2交于A(xA,yA)、O(0,0)两点,过点O与直线l垂直的直线交抛物线C于点B(xB,yB).如图所示.
(1)求抛物线C的焦点坐标;
(2)求经过A、B两点的直线与y轴交点M的坐标;
(3)过抛物线y=
x2的顶点任意作两条互相垂直的直线,过这两条直线与抛物线的交点A、B的直线AB是否恒过定点,如果是,指出此定点,并证明你的结论;如果不是,请说明理由.
| 1 |
| 4 |
(1)求抛物线C的焦点坐标;
(2)求经过A、B两点的直线与y轴交点M的坐标;
(3)过抛物线y=
| 1 |
| 4 |

(1)抛物线C:y=
x2的方程化为x2=4y,
∴2p=4,p=2.…(2分)
∴抛物线C的焦点坐标为(0,1).…(4分)
(2)联立方程组
,解得点A坐标为(8,16).…(6分)
联立方程组
,解得点B坐标为(-2,1).…(7分)
所以直线AB的方程为y-1=
•(x+2),…(8分)
令x=0,解得y=4.
∴点M的坐标为(0,4).…(9分)
(3)结论:过抛物线y=
x2的顶点任意作两条互相垂直的直线,
过这两条直线与抛物线的交点的直线AB恒过定点(0,4).…(10分)
证明如下:
设过抛物线y=
x2的顶点的一条直线为y=kx(k≠0),
则另一条为y=-
x,
联立方程组
,解得点A坐标为(4k,4k2).…(11分)
联立方程组
,解得点B坐标为(-
,
).…(12分)
所以直线AB的方程为y-
=
•(x+
),…(13分)
令x=0,解得y=4.
∴直线AB恒过定点(0,4).…(14分)
| 1 |
| 4 |
∴2p=4,p=2.…(2分)
∴抛物线C的焦点坐标为(0,1).…(4分)
(2)联立方程组
|
联立方程组
|
所以直线AB的方程为y-1=
| 16-1 |
| 8-(-2) |
令x=0,解得y=4.
∴点M的坐标为(0,4).…(9分)
(3)结论:过抛物线y=
| 1 |
| 4 |
过这两条直线与抛物线的交点的直线AB恒过定点(0,4).…(10分)
证明如下:
设过抛物线y=
| 1 |
| 4 |
则另一条为y=-
| 1 |
| k |
联立方程组
|
联立方程组
|
| 4 |
| k |
| 4 |
| k2 |
所以直线AB的方程为y-
| 4 |
| k2 |
4k2-
| ||
4k-(-
|
| 4 |
| k |
令x=0,解得y=4.
∴直线AB恒过定点(0,4).…(14分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目