题目内容
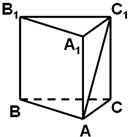
如图,边长为2的正方形A1ACC1绕直线CC1旋转90°得到正方形B1BCC1,D为CC1的中点,E为A1B的中点,G为△ADB的重心.
(1)求直线EG与直线BD所成的角;
(2)求直线A1B与平面ADB所成的角的正弦值.
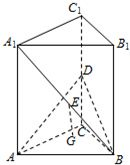
(1)求直线EG与直线BD所成的角;
(2)求直线A1B与平面ADB所成的角的正弦值.

由题设CC1⊥AC,CC1⊥BC,AC⊥BC
所以,以C为坐标原点,CA,CB,CC1所在直线为x,y,z轴,建立空间直角坐标系
则C(0,0,0),A(2,0,0),B(0,2,0),C1(0,0,2),A1(2,0,2),B1(0,2,2),
所以D(0,0,1),E(1,1,1),G(
,
,
).(2分)
(1)
=(-
,-
,-
),
=(0,-2,1)(4分)
所以
•
=
-
=0,
∴
⊥
所以,直线EG与直线BD所成的角为
.(5分)
(2)
=(-2,2,-2)(6分)
=(-2,2,0),
=(-2,0,1)
设
=(x0,y0,z0)为平面ABD的一个法向量
则
,
∴
取
=(1,1,2).(8分)
设A1B与平面ADB所成的角为θ
则sinθ=|cos?
>|=
=
.
即:A1B与平面ADB所成的角为正弦值为
.(10分)
所以,以C为坐标原点,CA,CB,CC1所在直线为x,y,z轴,建立空间直角坐标系
则C(0,0,0),A(2,0,0),B(0,2,0),C1(0,0,2),A1(2,0,2),B1(0,2,2),
所以D(0,0,1),E(1,1,1),G(
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
(1)
| EG |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| BD |
所以
| EG |
| BD |
| 2 |
| 3 |
| 2 |
| 3 |
∴
| EG |
| BD |
所以,直线EG与直线BD所成的角为
| π |
| 2 |
(2)
| A1B |
| AB |
| AD |
设
| n |
则
|
∴
|
取
| n |
设A1B与平面ADB所成的角为θ
则sinθ=|cos?
| A1B, |
| n |
| 4 | ||||
2
|
| ||
| 3 |
即:A1B与平面ADB所成的角为正弦值为
| ||
| 3 |

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目