题目内容
【题目】如图,设斜率为k(k>0)的直线l与椭圆C: ![]() +
+ ![]() =1交于A、B两点,且OA⊥OB.
=1交于A、B两点,且OA⊥OB. 
(Ⅰ)求直线l在y轴上的截距(用k表示);
(Ⅱ)求△AOB面积取最大值时直线l的方程.
【答案】解:(Ⅰ)设l:y=kx+t,A(x1 , y1),B(x2 , y2), ∵斜率为k(k>0)的直线l与椭圆C: ![]() +
+ ![]() =1交于A、B两点,且OA⊥OB,
=1交于A、B两点,且OA⊥OB,
∴∠AOB=90°,∴ ![]() ,
,
∴x1x2+(kx1+t)(kx2+t)=0,∴(1+k2)x1x2+kt(x1+x2)+t2=0,(*)
联立  ,消去y,得x2+3(kx+t)2=9,即(1+3k2)x2+6ktx+3t2﹣9=0,
,消去y,得x2+3(kx+t)2=9,即(1+3k2)x2+6ktx+3t2﹣9=0,
则 ![]() ,x1x2=
,x1x2= ![]() 三,且△>0,代入(*)
三,且△>0,代入(*)
从而得(1+k2)(3t2﹣9)﹣6k2t2+t2(1+3k2)=0,∴3t2﹣9﹣9k2+t2=0,
∴ ![]() ,∴t=±
,∴t=± ![]() ,
,
∴直线l在y轴上的截距为 ![]() 或﹣
或﹣ ![]() .
.
(Ⅱ)设△AOB的面积为S,O到直线l的距离为d,则S= ![]() |AB|d,
|AB|d,
而由(1)知d= ![]() ,且|AB|=
,且|AB|= ![]()
= 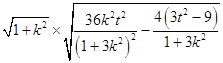 =
= ![]() =
=  ,
,
∴  ≤
≤ ![]() ,
,
当 ![]() 时,
时, ![]() ,解得k=
,解得k= ![]() ,∴t=
,∴t= ![]() ,
,
∴所求直线方程为y= ![]() 或y=
或y= ![]() .
.
【解析】(Ⅰ)设l:y=kx+t,A(x1 , y1),B(x2 , y2),由OA⊥OB,得(1+k2)x1x2+kt(x1+x2)+t2=0,联立  ,得x2+3(kx+t)2=9,即(1+3k2)x2+6ktx+3t2﹣9=0,由此利用韦达定理、根的判别式,结合已知条件能求出直线l在y轴上的截距.(Ⅱ)设△AOB的面积为S,O到直线l的距离为d,则S=
,得x2+3(kx+t)2=9,即(1+3k2)x2+6ktx+3t2﹣9=0,由此利用韦达定理、根的判别式,结合已知条件能求出直线l在y轴上的截距.(Ⅱ)设△AOB的面积为S,O到直线l的距离为d,则S= ![]() |AB|d,由此利用点到直线的距离公式和弦长公式能求出△AOB面积取最大值时直线l的方程.
|AB|d,由此利用点到直线的距离公式和弦长公式能求出△AOB面积取最大值时直线l的方程.
【考点精析】根据题目的已知条件,利用椭圆的标准方程的相关知识可以得到问题的答案,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.




