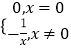题目内容
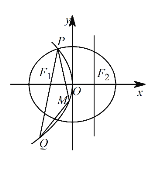
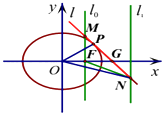
【题目】椭圆C: ![]() =1的右焦点F,过焦点F的直线l0⊥x轴,P(x0 , y0)(x0y0≠0)为C上任意一点,C在点P处的切线为l,l与l0相交于点M,与直线l1:x=3相交于N.
=1的右焦点F,过焦点F的直线l0⊥x轴,P(x0 , y0)(x0y0≠0)为C上任意一点,C在点P处的切线为l,l与l0相交于点M,与直线l1:x=3相交于N.
(I) 求证;直线 ![]() =1是椭圆C在点P处的切线;
=1是椭圆C在点P处的切线;
(Ⅱ)求证: ![]() 为定值,并求此定值;
为定值,并求此定值;
(Ⅲ)请问△ONP(O为坐标原点)的面积是否存在最小值?若存在,请求出最小及此时点P的坐标;若不存在,请说明理由.
【答案】证明:(Ⅰ)∵P(x0 , y0)在椭圆C: ![]() 上,
上,
∴ ![]() ,即
,即 ![]() ,
,
∴直线 ![]() 过点P(x0 , y0),
过点P(x0 , y0),
由 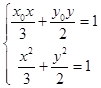 ,消去y,并利用
,消去y,并利用 ![]() ,得
,得 ![]() ,
,
即6x2﹣12x0x+6x02=0,即6(x﹣x0)2=0,∴x=x0 ,
∴直线 ![]() =1与椭圆C在点P处有且仅有一个交点,
=1与椭圆C在点P处有且仅有一个交点,
综上,直线 ![]() 是椭圆C在点P处的切线.
是椭圆C在点P处的切线.
(Ⅱ)在 ![]() 中,令x=1,得y=
中,令x=1,得y= ![]() ,∴M(1,
,∴M(1, ![]() ),
),
在 ![]() 中,令x=3,得y=
中,令x=3,得y= ![]() ,∴N(3,
,∴N(3, ![]() ),
),
又F(1,0),∴|FM|=| ![]() |=2|
|=2| ![]() |,
|,
|FN|= 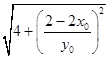 =2
=2 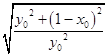 =2
=2 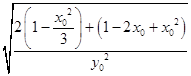 =2
=2 ![]() ,
,
∴ ![]() =
= ![]() 为定值.
为定值.
解:(Ⅲ)在直线 ![]() 中,令y=0,得x=
中,令y=0,得x= ![]() ,
,
∴切线l与x轴的交点为G( ![]() ,0),
,0),
S△ONP= 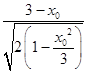 =
= 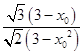 =
= 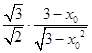
= ![]() |
| ![]() ||
|| ![]() |
|
= ![]() |
| ![]() ||
|| ![]() |
|
= 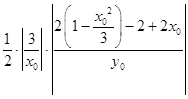
=| ![]() |=
|= ![]() ,
,
S△ONP= 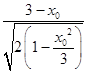 =
= 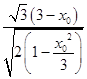 =
= 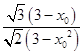 =
= 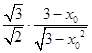 ,
,
令3﹣x0= ![]() ,由﹣
,由﹣ ![]() ,得
,得 ![]() ,且t
,且t ![]() ,
,
且 ![]() =
= 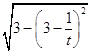 =
= ![]() =
= ![]()
![]() =
= 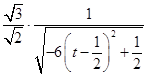 ,
,
∴当t= ![]() ,x0=1时,△ONP(O为坐标原点)的面积是存在最小值{S△ONP}min=
,x0=1时,△ONP(O为坐标原点)的面积是存在最小值{S△ONP}min= ![]() ,
,
此时P(1, ![]() ).
).
【解析】(Ⅰ)推导出直线 ![]() 过点P(x0 , y0),由
过点P(x0 , y0),由 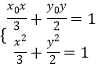 及
及 ![]() ,得
,得 ![]() ,由此能证明直线
,由此能证明直线 ![]() 是椭圆C在点P处的切线.(Ⅱ)在
是椭圆C在点P处的切线.(Ⅱ)在 ![]() 中,令x=1,M(1,
中,令x=1,M(1, ![]() ),令x=3,得N(3,
),令x=3,得N(3, ![]() ),由此求出|FM|,|FN|,由此能证明
),由此求出|FM|,|FN|,由此能证明 ![]() 为定值.(Ⅲ)求出切线l与x轴的交点为G(
为定值.(Ⅲ)求出切线l与x轴的交点为G( ![]() ,0),推导出S△ONP=
,0),推导出S△ONP= ![]() =
= ![]() ,令3﹣x0=
,令3﹣x0= ![]() ,利用配方法能求出△ONP的面积的最小值及对应的P点坐标.
,利用配方法能求出△ONP的面积的最小值及对应的P点坐标.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校在高二年级实行选课走班教学,学校为学生提供了多种课程,其中数学科提供5种不同层次的课程,分别称为数学1、数学2、数学3、数学4、数学5,每个学生只能从这5种数学课程中选择一种学习,该校高二年级1800名学生的数学选课人数统计如表:
课程 | 数学1 | 数学2 | 数学3 | 数学4 | 数学5 | 合计 |
选课人数 | 180 | 540 | 540 | 360 | 180 | 1800 |
为了了解数学成绩与学生选课情况之间的关系,用分层抽样的方法从这1800名学生中抽取了10人进行分析.
(1)从选出的10名学生中随机抽取3人,求这3人中至少有2人选择数学2的概率;
(2)从选出的10名学生中随机抽取3人,记这3人中选择数学2的人数为X,选择数学1的人数为Y,设随机变量ξ=X﹣Y,求随机变量ξ的分布列和数学期望E(ξ).