Question

【题目】已知函数f（x）的定义域为R．a，b∈R，若此函数同时满足：
①当a+b=0时，有f（a）+f（b）=0；
②当a+b＞0时，有f（a）+f（b）＞0，
则称函数f（x）为Ω函数．
在下列函数中：
①y=x+sinx；
②y=3x﹣（ ）x；
③y=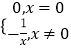
是Ω函数的为 ． （填出所有符合要求的函数序号）

Answer 1

【答案】①②
【解析】解：容易判断①②③都是奇函数；
y′=1﹣cosx≥0，y′=ln3（3x+3﹣x）＞0；
∴①②都在定义域R上单调递增；
③在定义域R上没有单调性；
设y=f（x），从而对于函数①②：a+b=0时，a=﹣b，f（a）=f（﹣b）=﹣f（b）；
∴f（a）+f（b）=0；
a+b＞0时，a＞﹣b；
∴f（a）＞f（﹣b）=﹣f（b）；
∴f（a）+f（b）＞0；
∴①②是Ω函数；
对于函数③，a+b＞0时，得到a＞﹣b；
∵f（x）不是增函数；
∴得不到f（a）＞f（﹣b），即得不出f（a）+f（b）＞0．
所以答案是：①②．
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点，需要掌握两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系才能正确解答此题．