题目内容
【题目】如图,PA⊥平面ABC,AE⊥PB,AB⊥BC,AF⊥PC,PA=AB=BC.
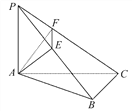
(1)求证:平面AEF⊥平面PBC.
(2)求二面角P-BC-A的大小.
【答案】(1)详见解析(2)![]()
【解析】试题分析:(1)由线面垂直的定义,根据PA⊥平面ABC得PA⊥BC,结合AB⊥BC得BC⊥平面PAB,从而得出AE⊥BC,结合AE⊥PB证出AE⊥平面PBC,最后根据面面垂直判定定理,即可证出平面AEF⊥平面PBC;
(2)由(1)的结论得BC⊥AB且BC⊥PB,所以∠PBA是二面角P﹣BC﹣A的平面角,Rt△PAB中算出∠PBA=45°,即可得到二面角P﹣BC﹣A的大小。
试题解析:
(1)因为PA⊥平面ABC,又BC平面ABC,所以PA⊥BC,
又AB⊥BC,AB与PA相交于点A,
所以BC⊥平面PAB,又AE平面PAB,所以BC⊥AE,又AE⊥PB,而PB与BC相交于点B,所以AE⊥平面PBC,又AE平面AEF,故平面AEF⊥平面PBC.
(2)由(1)知,BC⊥平面PAB,PB平面PAB,
所以PB⊥BC,又AB⊥BC,
所以∠PBA就是二面角P-BC-A的平面角,
在Rt△PAB中,因为PA=AB,所以∠PBA=45°,
即二面角P-BC-A的大小为45°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目