Question

【题目】比较下列各组数中两个数的大小．

(1) 与；

(2)3与3.1；

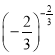(3) 与；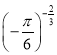

(4)0.20.6与0.30.4.

Answer 1

【答案】(1) > (2)3>3.1 (3) < 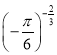(4)0.20.6<0.30.4.

【解析】试题分析：（1）借助于函数y＝在(0，＋∞)上单调递增，即可比较大小；

（2）借助于y＝在(0，＋∞)上为减函数，即可比较大小；

（3）借助于中间变量0.20.4，易知0.20.6<0.20.4，0.20.4<0.30.4.

试题解析：

(1)函数y＝在(0，＋∞)上单调递增，

又>，∴ >.

(2)y＝在(0，＋∞)上为减函数，

又3<3.1，∴3>3.1

(3)函数y＝在(0，＋∞)上为减函数，

又>，

∴<.

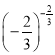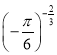(4)函数取中间值0.20.4，函数y＝0.2x在(0，＋∞)上为减函数，所以0.20.6<0.20.4；

又函数y＝x0.4在(0，＋∞)为增函数，所以0.20.4<0.30.4.

∴0.20.6<0.30.4.

点睛: 本题考查幂函数的图象和性质,属于基础题.幂函数的图象一定在第一象限内，一定不在第四象限，至于是否在第二、三象限内，要看函数的奇偶性；幂函数的图象最多只能同时在两个象限内；如果幂函数图象与坐标轴相交，则交点一定是原点．对于函数f(x)＝xα,当时,函数在单调递减;当时,函数在单调递增;当时,函数为常函数.