题目内容
6.函数y=cos2x-sin2x的图象可以由函数y=cos2x+sin2x的图象经过下列哪种变换得到( )| A. | 向右平移$\frac{3π}{4}$ | B. | 向右平移π | C. | 向左平移$\frac{π}{2}$ | D. | 向左平移π |
分析 根据函数y=cos2x+sin2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$),y=cos2x-sin2x=$\sqrt{2}$sin($\frac{π}{4}-2x$),利用y=Asin(ωx+φ)的图象变化规律,可得结论.
解答 解:∵y=cos2x+sin2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$),y=cos2x-sin2x=$\sqrt{2}$sin($\frac{π}{4}-2x$),
又∵y=$\sqrt{2}$sin[2(x-$\frac{3π}{4}$)+$\frac{π}{4}$]=$\sqrt{2}$sin(2x-$\frac{5π}{4}$)=-$\sqrt{2}$sin(π+$\frac{π}{4}$-2x)=$\sqrt{2}$sin($\frac{π}{4}-2x$),
∴函数y=cos2x+sin2x的图象向右平移$\frac{3π}{4}$可得函数y=cos2x-sin2x的图象.
故选:A.
点评 本题主要考查两角和差的正弦公式,y=Asin(ωx+φ)的图象变化规律,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.在区间(-1,1)上单调递增且为奇函数的是( )
| A. | y=ln(x+1) | B. | y=xsinx | C. | y=x-x3 | D. | y=3x+sinx |
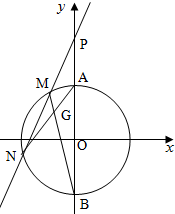 已知A,B为圆O:x2+y2=4与y轴的交点(A在B上),过点P(0,4)的直线l交圆O于M,N两点.
已知A,B为圆O:x2+y2=4与y轴的交点(A在B上),过点P(0,4)的直线l交圆O于M,N两点. 如图,有一景区的平面图是一个半圆形,其中O为圆心,直径AB的长为2km,C,D两点在半圆弧上,且BC=CD,设∠COB=θ;
如图,有一景区的平面图是一个半圆形,其中O为圆心,直径AB的长为2km,C,D两点在半圆弧上,且BC=CD,设∠COB=θ;