题目内容
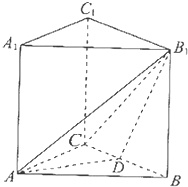
正方体ABCD-A1B1C1D1的棱长为1,E、G分别是BC、C1D1的中点
(1)求证:EG∥平面BDD1B1
(2)求E到平面BDD1B1的距离.

(1)求证:EG∥平面BDD1B1
(2)求E到平面BDD1B1的距离.

(1)取BD的中点F,连结EF,D1F,
∵E为BC的中点,
∴EF为三角形BCD的中位线,
则EF∥DC,且EF=
CD,
∵G为C1D1的中点,
∴D1G∥CD,且D1G=
CD,
∴EF∥D1C,且EF=D1G,
∴四边形EFD1G为平行四边形,
∴D1F∥EG,而D1F?平面BB1D1D,EG?平面BB1D1D,
∴EG∥平面BB1D1D.
(2)∵EG∥平面BDD1B1,则G到平面BDD1B1的距离,即为E到平面BDD1B1的距离.
∴过G作GN⊥B1D1于N,则GN⊥面BDD1B1,
∵G是C1D1的中点,
∴D1G=
,
又sin45°=
=
,
∴GN=
×
=
.
即E到平面BDD1B1的距离为
.
∵E为BC的中点,
∴EF为三角形BCD的中位线,
则EF∥DC,且EF=
| 1 |
| 2 |
∵G为C1D1的中点,
∴D1G∥CD,且D1G=
| 1 |
| 2 |

∴EF∥D1C,且EF=D1G,
∴四边形EFD1G为平行四边形,
∴D1F∥EG,而D1F?平面BB1D1D,EG?平面BB1D1D,
∴EG∥平面BB1D1D.
(2)∵EG∥平面BDD1B1,则G到平面BDD1B1的距离,即为E到平面BDD1B1的距离.
∴过G作GN⊥B1D1于N,则GN⊥面BDD1B1,
∵G是C1D1的中点,
∴D1G=
| 1 |
| 2 |
又sin45°=
| GN |
| D1G |
| ||
| 2 |
∴GN=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
即E到平面BDD1B1的距离为
| ||
| 4 |

练习册系列答案
相关题目