题目内容
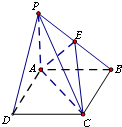
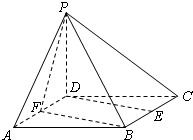
如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
(1)求证:BE∥平面PDF;
(2)求证:平面PDF⊥平面PAB;
(3)求二面角P-BC-A的大小.
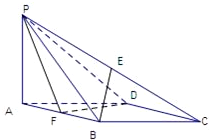
(1)求证:BE∥平面PDF;
(2)求证:平面PDF⊥平面PAB;
(3)求二面角P-BC-A的大小.

证明:(1)取PD的中点M,
∵E是PC的中点
∴ME是△PCD的中位线
∴ME∥FB
∴四边形MEBF是平行四边形∴BE∥MF
∵BE?平面PDF,MF?平面PDF
∴BE∥平面PDF.
(2)连接BD,易得△ABD为等边三角形
又由F为AB的中点
∴DF⊥AB
又∵PA⊥平面ABCD,
∴PA⊥DF
又由PA∩AB=A
∴DF⊥平面PAB
又∵DF?平面PDF
∴平面PDF⊥平面PAB.
(3)过点A做AH⊥CB延长线于H,因为PA⊥面ABCD,所以PH⊥BC,既∠PHA为二面角P-BC-A的平面角,
在Rt△ABC中PA=1,AH=
,所以∠PHA=30°
既二面角P-BC-A的大小为30°.
∵E是PC的中点
∴ME是△PCD的中位线
∴ME∥FB
∴四边形MEBF是平行四边形∴BE∥MF
∵BE?平面PDF,MF?平面PDF
∴BE∥平面PDF.
(2)连接BD,易得△ABD为等边三角形
又由F为AB的中点
∴DF⊥AB
又∵PA⊥平面ABCD,
∴PA⊥DF
又由PA∩AB=A
∴DF⊥平面PAB
又∵DF?平面PDF
∴平面PDF⊥平面PAB.
(3)过点A做AH⊥CB延长线于H,因为PA⊥面ABCD,所以PH⊥BC,既∠PHA为二面角P-BC-A的平面角,
在Rt△ABC中PA=1,AH=
| 3 |
既二面角P-BC-A的大小为30°.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目