题目内容
已知 的图像上相邻两对称轴的距离为
的图像上相邻两对称轴的距离为 .
.
(1)若 ,求
,求 的递增区间;
的递增区间;
(2)若 时,
时, 的最大值为4,求
的最大值为4,求 的值.
的值.
(1) ;(2)
;(2) .
.
解析试题分析:首先利用二倍角公式与两角和差公式进行化简可得 ,然后对两相邻对称轴的距离可求得
,然后对两相邻对称轴的距离可求得 ,(1)由正弦函数的单调增区间可求出函数
,(1)由正弦函数的单调增区间可求出函数 的递增区间;(2)由题中所给
的递增区间;(2)由题中所给 的范围,求出整体
的范围,求出整体 的范围,再结合
的范围,再结合 的图像,不难求得
的图像,不难求得 的取值范围,即可求出
的取值范围,即可求出 的最大值,再利用所给最大值4,可求出
的最大值,再利用所给最大值4,可求出 的值.
的值.
试题解析:由 3分
3分
因为 的图像上相邻对称轴的距离为
的图像上相邻对称轴的距离为 ,故
,故 5分
5分 6分
6分
(1)由 可解得
可解得
故 的增区间是
的增区间是 9分
9分
(2)当 时,
时,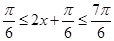 10分
10分 11分
11分
 12分
12分
考点:1.二倍角公式和两角和差公式;2.三角函数的图像及性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,角A,B,C所对的边分别为a,b,c,已知
中,角A,B,C所对的边分别为a,b,c,已知 .
. ,且
,且 时,求a的值;
时,求a的值; 时,求
时,求 的值.
的值. ,
,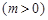 的最大值为2.
的最大值为2.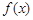 在
在 上的值域;
上的值域; 外接圆半径
外接圆半径 ,
, ,角
,角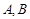 所对的边分别是
所对的边分别是 ,求
,求 的值.
的值. ,记函数
,记函数 的最小正周期为
的最小正周期为 ,向量
,向量 ,
, (
( ),且
),且 .
. 在区间
在区间 上的最值;
上的最值; 的值.
的值. (
( ).求:
).求: 的值域,并写出
的值域,并写出 ,求
,求 ;
; 为第二象限角,化简
为第二象限角,化简 .
. .
. 时,求
时,求 值;
值; (
( 且
且 ),使得
),使得 在
在 的最小值.
的最小值. 的最小正周期为
的最小正周期为 .
. 的对称轴方程;
的对称轴方程;  ,求
,求 的值.
的值. 的顶点在原点,始边与x轴正半轴重合,终边为射线4x+3y=0(x≥0),求5sin
的顶点在原点,始边与x轴正半轴重合,终边为射线4x+3y=0(x≥0),求5sin .其中
.其中 .
.