题目内容
已知函数 ,
,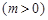 的最大值为2.
的最大值为2.
(Ⅰ)求函数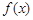 在
在 上的值域;
上的值域;
(Ⅱ)已知 外接圆半径
外接圆半径 ,
, ,角
,角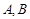 所对的边分别是
所对的边分别是 ,求
,求 的值.
的值.
(Ⅰ)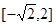 (Ⅱ)
(Ⅱ)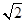
解析试题分析:(Ⅰ)函数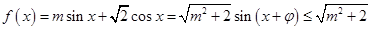 ,
,
解方程: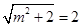 ,解得
,解得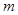 的值,再根据的
的值,再根据的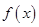 单调性求其值域.
单调性求其值域.
(Ⅱ)利用(Ⅰ)的结果将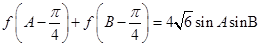 ,再利用正弦定理将其转化为边长
,再利用正弦定理将其转化为边长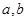 的关系,从而求出
的关系,从而求出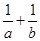 的值.
的值.
试题解析:解:(1)由题意,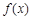 的最大值为
的最大值为 ,所以
,所以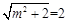 . 2分
. 2分
而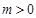 ,于是
,于是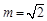 ,
,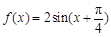 . 4分
. 4分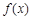 在
在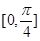 上递增.在
上递增.在 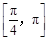 递减,
递减,
所以函数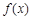 在
在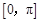 上的值域为
上的值域为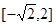 ; 5分
; 5分
(Ⅱ)化简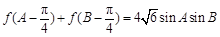 得
得 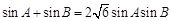 . 7分
. 7分
由正弦定理,得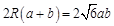 , 9分
, 9分
因为△ABC的外接圆半径为 .
.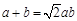 . 11分
. 11分
所以 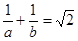 12分
12分
考点:1、三角函数的性质;2、正弦定理.

练习册系列答案
相关题目
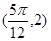 在函数
在函数 的图象上,直线
的图象上,直线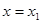 、
、 是
是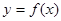 图象的任意两条对称轴,且
图象的任意两条对称轴,且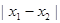 的最小值为
的最小值为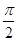 .
.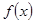 的单递增区间和其图象的对称中心坐标;
的单递增区间和其图象的对称中心坐标;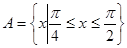 ,
,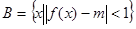 ,若
,若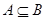 ,求实数
,求实数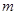 的取值范围.
的取值范围. sin x,1),n=(cos x,-y),且m⊥n.
sin x,1),n=(cos x,-y),且m⊥n.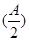 =3,且a=2,b+c=4,求△ABC的面积.
=3,且a=2,b+c=4,求△ABC的面积.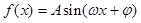 (其中
(其中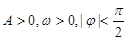 )的部分图象如图所示.
)的部分图象如图所示.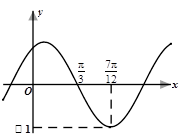
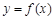 的解析式;
的解析式;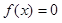 的解集.
的解集.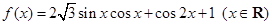 .
.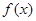 的最小正周期;
的最小正周期;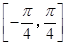 上的最小值,并写出
上的最小值,并写出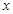 值.
值. .
. 的值;
的值; 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.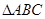 中,
中,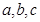 分别为角
分别为角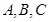 的对边,
的对边,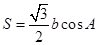
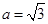 ,设角B的大小为x,用x表示c,并求c的取值范围.
,设角B的大小为x,用x表示c,并求c的取值范围. 的图像上相邻两对称轴的距离为
的图像上相邻两对称轴的距离为 .
. ,求
,求 的递增区间;
的递增区间; 时,
时, 的值.
的值.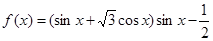 .
. 的单调递减区间;
的单调递减区间;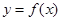 的图像向左平移
的图像向左平移 个单位,再将得到的图像横坐标变为原来的2倍(纵坐标不变)后得到
个单位,再将得到的图像横坐标变为原来的2倍(纵坐标不变)后得到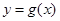 的图像,若
的图像,若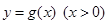 的图像与直线
的图像与直线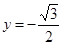 交点的横坐标由小到大依次是
交点的横坐标由小到大依次是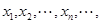 求数列
求数列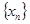 的前2n项的和。
的前2n项的和。