题目内容
已知 (
( ).求:
).求:
(1)若 ,求
,求 的值域,并写出
的值域,并写出 的单调递增区间;
的单调递增区间;
(2)若 ,求
,求 的值域.
的值域.
(1)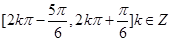 ;(2)(-1,2]
;(2)(-1,2]
解析试题分析:(1)通过三角函数的化一公式将函数 化为
化为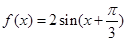 .再根据函数
.再根据函数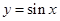 的单调递增区间
的单调递增区间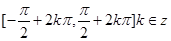 ,使得
,使得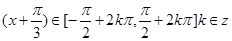 ,即可求出
,即可求出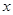 的范围.
的范围.
(2)由(1)可知函数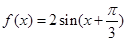 所以因为
所以因为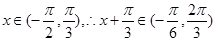 通过函数
通过函数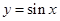 .
.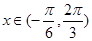 的单调性即可得函数
的单调性即可得函数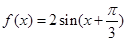 的值域.
的值域.
试题解析:(1)化简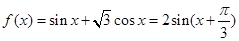 .所以
.所以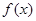 的值域为[-2,2].函数的单调区间为
的值域为[-2,2].函数的单调区间为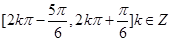 .
.
(2)因为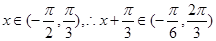 .
. 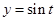 在
在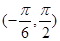 上递增,在
上递增,在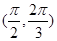 上递减.所以
上递减.所以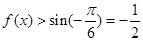 .
. 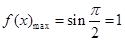 .所以
.所以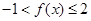 .所以
.所以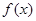 的值域为(-1,2]
的值域为(-1,2]
考点:1.函数的化一公式.2.复合三角函数的单调性.3.复合三角函数的值域的求法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (弦´矢+矢2).弧田(如图),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.
(弦´矢+矢2).弧田(如图),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差. ,弦长等于9米的弧田.
,弦长等于9米的弧田.
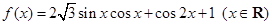 .
.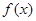 的最小正周期;
的最小正周期;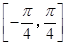 上的最小值,并写出
上的最小值,并写出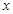 值.
值.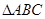 中,
中,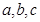 分别为角
分别为角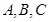 的对边,
的对边,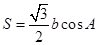
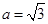 ,设角B的大小为x,用x表示c,并求c的取值范围.
,设角B的大小为x,用x表示c,并求c的取值范围.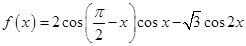 ,
,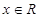 .
.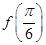 的值;
的值;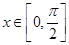 时,求
时,求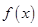 的最值.
的最值. 的图像上相邻两对称轴的距离为
的图像上相邻两对称轴的距离为 .
. ,求
,求 的递增区间;
的递增区间; 时,
时, 的值.
的值.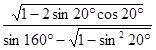 ;
;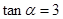 ,求
,求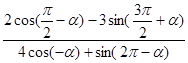 的值.
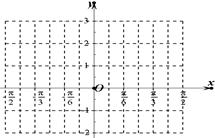
的值. .
.
 的最小值及取最小值时
的最小值及取最小值时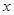 的集合;
的集合;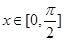 时的值域;
时的值域;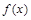 在区间
在区间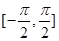 上的图像(要求列表,描点).
上的图像(要求列表,描点).