题目内容
已知函数 和函数
和函数 ,
,
(1)证明:只要 ,无论b取何值,函数
,无论b取何值,函数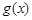 在定义域内不可能总为增函数;
在定义域内不可能总为增函数;
(2)在同一函数图象上任意取不同两点 ,线段AB的中点为
,线段AB的中点为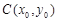 ,记直线AB的斜率为
,记直线AB的斜率为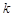 ,①对于函数
,①对于函数 ,求证:
,求证: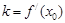 ;②对于函数
;②对于函数 ,是否具有与①同样的性质?证明你的结论.
,是否具有与①同样的性质?证明你的结论.
 和函数
和函数 ,
,(1)证明:只要
 ,无论b取何值,函数
,无论b取何值,函数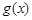 在定义域内不可能总为增函数;
在定义域内不可能总为增函数;(2)在同一函数图象上任意取不同两点
 ,线段AB的中点为
,线段AB的中点为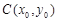 ,记直线AB的斜率为
,记直线AB的斜率为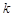 ,①对于函数
,①对于函数 ,求证:
,求证: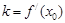 ;②对于函数
;②对于函数 ,是否具有与①同样的性质?证明你的结论.
,是否具有与①同样的性质?证明你的结论.证明:(1)若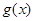 在
在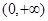 上是增函数,则
上是增函数,则 恒成立,从而必有
恒成立,从而必有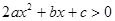 在
在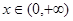 上恒成立。
上恒成立。
因为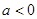 由二次函数的性质可知
由二次函数的性质可知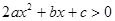 不可能恒成立,因此函数
不可能恒成立,因此函数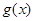 在定义域内不可能总为增函数。
在定义域内不可能总为增函数。
(2)①对于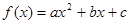 有,
有,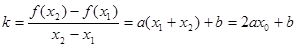 。又因为
。又因为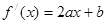 ,所以
,所以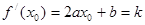 成立。
成立。
②对于函数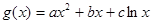 ,不妨设
,不妨设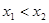 ,则
,则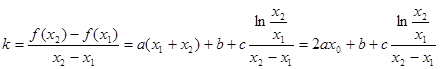 。
。
又因为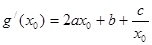 ,如果有①的性质,则
,如果有①的性质,则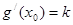 ,即有
,即有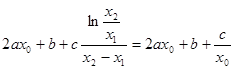 ,化简得
,化简得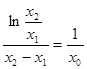 ,也就是
,也就是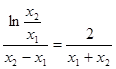
令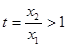 ,则
,则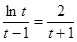 。设
。设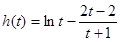 ,则
,则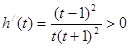 ,所以
,所以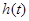 在
在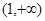 上单调递增,
上单调递增,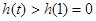 ,故
,故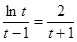 不可能成立,从而
不可能成立,从而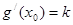 不成立,因此函数
不成立,因此函数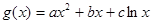 不具有与①同样的性质。
不具有与①同样的性质。
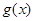 在
在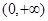 上是增函数,则
上是增函数,则 恒成立,从而必有
恒成立,从而必有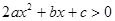 在
在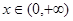 上恒成立。
上恒成立。因为
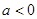 由二次函数的性质可知
由二次函数的性质可知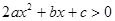 不可能恒成立,因此函数
不可能恒成立,因此函数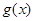 在定义域内不可能总为增函数。
在定义域内不可能总为增函数。(2)①对于
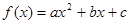 有,
有,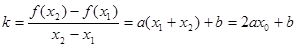 。又因为
。又因为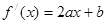 ,所以
,所以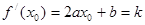 成立。
成立。②对于函数
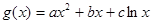 ,不妨设
,不妨设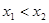 ,则
,则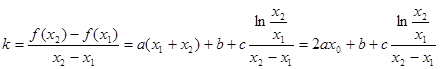 。
。又因为
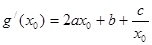 ,如果有①的性质,则
,如果有①的性质,则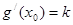 ,即有
,即有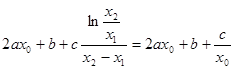 ,化简得
,化简得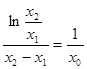 ,也就是
,也就是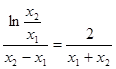
令
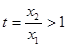 ,则
,则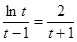 。设
。设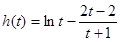 ,则
,则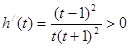 ,所以
,所以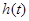 在
在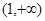 上单调递增,
上单调递增,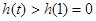 ,故
,故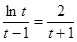 不可能成立,从而
不可能成立,从而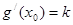 不成立,因此函数
不成立,因此函数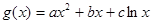 不具有与①同样的性质。
不具有与①同样的性质。略

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
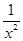 .
.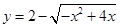 的值域是( )
的值域是( )



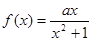
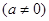 ,
,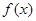 的奇偶性;
的奇偶性;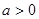 时,判断
时,判断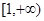 上的单调性并给出证明。
上的单调性并给出证明。 是(-∞,+∞)上的减函数,那么a的取值范围是
是(-∞,+∞)上的减函数,那么a的取值范围是 )
)  ,
,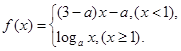 是
是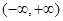 上的增函数,那么实数a的取值范围是( )
上的增函数,那么实数a的取值范围是( )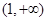
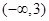
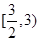
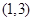
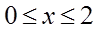 ,求函数
,求函数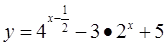 的最大值与最小值。
的最大值与最小值。 的值域是
的值域是 ,+
,+ )
) ,1)
,1)