题目内容
已知数列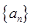 具有性质:①
具有性质:①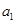 为整数;②对于任意的正整数
为整数;②对于任意的正整数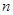 ,当
,当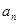 为偶数时,
为偶数时,
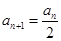 ;当
;当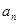 为奇数时,
为奇数时,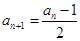 .
.
(1)若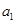 为偶数,且
为偶数,且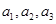 成等差数列,求
成等差数列,求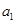 的值;
的值;
(2)设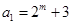 (
(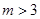 且
且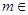 N),数列
N),数列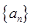 的前
的前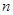 项和为
项和为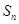 ,求证:
,求证: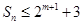 ;
;
(3)若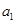 为正整数,求证:当
为正整数,求证:当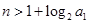 (
(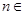 N)时,都有
N)时,都有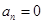 .
.
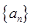 具有性质:①
具有性质:①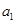 为整数;②对于任意的正整数
为整数;②对于任意的正整数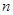 ,当
,当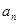 为偶数时,
为偶数时,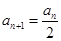 ;当
;当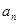 为奇数时,
为奇数时,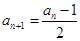 .
.(1)若
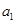 为偶数,且
为偶数,且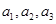 成等差数列,求
成等差数列,求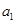 的值;
的值;(2)设
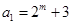 (
(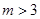 且
且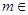 N),数列
N),数列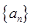 的前
的前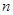 项和为
项和为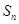 ,求证:
,求证: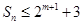 ;
;(3)若
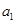 为正整数,求证:当
为正整数,求证:当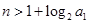 (
(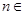 N)时,都有
N)时,都有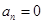 .
.(1) 是奇数,则
是奇数,则 ,
, ,
, 若
若 是偶数,则
是偶数,则 ,
,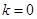 ,
,
(2)根据数列的求和公式来证明不等式
(3)要证明对于当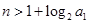 (
(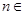 N)时,都有
N)时,都有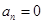 .,则要对于其通项公式分情况来得到其通项公式的表达式证明。
.,则要对于其通项公式分情况来得到其通项公式的表达式证明。
 是奇数,则
是奇数,则 ,
, ,
, 若
若 是偶数,则
是偶数,则 ,
,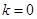 ,
,
(2)根据数列的求和公式来证明不等式
(3)要证明对于当
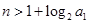 (
(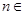 N)时,都有
N)时,都有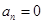 .,则要对于其通项公式分情况来得到其通项公式的表达式证明。
.,则要对于其通项公式分情况来得到其通项公式的表达式证明。试题分析:⑴设
 ,
, ,则:
,则: ,
,
分两种情况:
 是奇数,则
是奇数,则 ,
, ,
,
若
 是偶数,则
是偶数,则 ,
,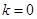 ,
,
⑵当
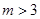 时,
时,

∴

⑶∵
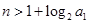 ,∴
,∴ ,∴
,∴
由定义可知:
 ∴
∴
∴

∴
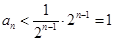
∵
 ,∴
,∴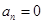 ,
,综上可知:当
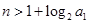
 时,都有
时,都有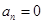
点评:本试题主要是考查了等差数列和数列的求和,以及数列与不等式的证明,属于中档题。

练习册系列答案
相关题目
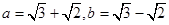 ,则
,则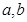 的等差中项为( )
的等差中项为( )



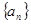 的公差为2,若
的公差为2,若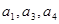 成等比数列, 则
成等比数列, 则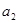 =( )
=( )



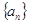 的首项为1,其前n项和为
的首项为1,其前n项和为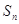 ,
,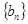 是公比为正整数的等比数列,其首项为3,前n项和为
是公比为正整数的等比数列,其首项为3,前n项和为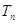 . 若
. 若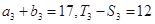 .
.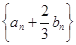 的前n项和
的前n项和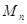 .(5分)
.(5分)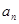 }是等差数列,
}是等差数列,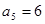 ,
,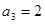 时,若自然数
时,若自然数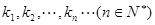 满足
满足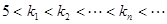 ,使得
,使得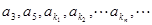 成等比数列,(1)求数列{
成等比数列,(1)求数列{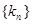 的通项公式及其前n项的和
的通项公式及其前n项的和 .
. 满足
满足 ,
,  (
( ),则
),则 =
= 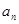 }中,a1=3,
}中,a1=3,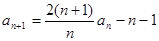 ,
,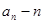 关于n的表达式(不用证明);
关于n的表达式(不用证明);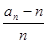 }是什么类型的数列并证明;
}是什么类型的数列并证明; 为等差数列,若
为等差数列,若 ,则
,则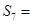 .
.