题目内容
【题目】如图,已知三棱柱![]() 的侧棱垂直于底面,
的侧棱垂直于底面,![]()
![]() ,点
,点![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.
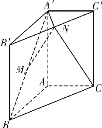
(1)证明:![]() 平面
平面![]() ;
;
(2)设![]() ,当
,当![]() 为何值时,
为何值时,![]() 平面
平面![]() ,试证明你的结论.
,试证明你的结论.
【答案】(Ⅰ)证明见解析(Ⅱ)![]() 时,
时,![]()
【解析】
试题(1)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;(2)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化.
试题解析:
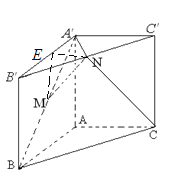
(Ⅰ)取![]() 得中点
得中点![]() ,连接
,连接![]() ,因为
,因为![]() 分别为
分别为![]() 和
和![]() 的中点,
的中点,
所以![]() 又因为
又因为![]() ,
,![]() ,
,
所以![]() ,
,![]() , 5分
, 5分
所以![]() ,因为
,因为![]() ,
,
所以![]() ; 6分
; 6分
(Ⅱ)连接![]() ,设
,设![]() ,则
,则![]() ,
,
由题意知![]()
因为三棱柱![]() 侧棱垂直于底面,
侧棱垂直于底面,
所以![]() ,
,
因为![]() ,点
,点![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,
![]() , 9分
, 9分
要使![]() ,
,
只需![]() 即可,
即可,
所以![]() ,即
,即![]() ,
,
则![]() 时,
时,![]() . 12分
. 12分

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案【题目】某校针对校食堂饭菜质量开展问卷调查,提供满意与不满意两种回答,调查结果如下表(单位:人):
学生 | 高一 | 高二 | 高三 |
满意 | 500 | 600 | 800 |
不满意 | 300 | 200 | 400 |
(1)求从所有参与调查的人中任选1人是高三学生的概率;
(2)从参与调查的高三学生中,用分层抽样的方法抽取6人,在这6人中任意选取2人,求这两人对校食堂饭菜质量都满意的概率.
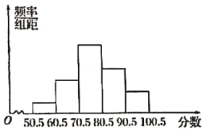
【题目】随着手机的普及,大学生迷恋手机的现象非常严重.为了调查双休日大学生使用手机的时间,某机构采用不记名方式随机调查了使用手机时间不超过10小时的50名大学生,将50人使用手机的时间分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别加以统计,得到下表,根据数据完成下列问题:
分别加以统计,得到下表,根据数据完成下列问题:
使用时间/时 |
|
|
|
|
|
大学生/人 | 5 | 10 | 15 | 12 | 8 |

(1)完成频率分布直方图,并根据频率分布直方图估计大学生使用手机时间的中位数(保留小数点后两位);
(2)用分层抽样的方法从使用手机时间在区间![]() ,
,![]() ,
,![]() 的大学生中抽取6人,再从这6人中随机抽取2人,求这2人取自不同使用时间区间的概率.
的大学生中抽取6人,再从这6人中随机抽取2人,求这2人取自不同使用时间区间的概率.