题目内容
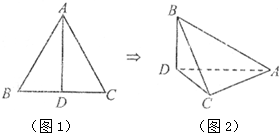 已知正三角形ABC的边长为2,沿着BC边上的高AD将正三角形折起,使得平面ABD⊥平面ACD(如图),则三棱锥A-BCD的体积为
已知正三角形ABC的边长为2,沿着BC边上的高AD将正三角形折起,使得平面ABD⊥平面ACD(如图),则三棱锥A-BCD的体积为
| ||
| 6 |
| ||
| 6 |
分析:根据题意,证出AD⊥平面BCD且∠BDC=90°.正三角形中算出BD=CD=1且AD=
,得到△BCD的面积S△BCD=
,利用锥体的体积公式即可算出三棱锥A-BCD的体积.
| 3 |
| 1 |
| 2 |
解答:解:∵AD⊥BD,AD⊥CD,BD∩CD=D
∴AD⊥平面BCD,
∵平面ABD⊥平面ACD,且∠BDC是二面角B-AD-C的平面角
∴∠BDC=90°,
∵AD是边长为2的正三角形的高,可得BD=CD=1,AD=
∴△BCD的面积S△BCD=
×1×1=
因此三棱锥A-BCD的体积V=
×S△BCD×AD=
×
×
=
故答案为:
∴AD⊥平面BCD,
∵平面ABD⊥平面ACD,且∠BDC是二面角B-AD-C的平面角
∴∠BDC=90°,
∵AD是边长为2的正三角形的高,可得BD=CD=1,AD=
| 3 |
∴△BCD的面积S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
因此三棱锥A-BCD的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 6 |
故答案为:
| ||
| 6 |
点评:本题给出平面图形的折叠,求三棱锥A-BCD的体积.着重考查了正三角形的性质、线面垂直的判定与性质和锥体体积求法等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知正三角形ABC的边长为a,那么三角形ABC根据斜二测画法得到的平面直观图三角形A′B′C′的面积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知正三角形ABC的边长为1,且
=
,
=
,则|
-
|=( )
| BA |
| a |
| AC |
| b |
| a |
| b |
A、
| ||
| B、3 | ||
C、
| ||
| D、1 |
 如图,已知正三角形ABC的边长为2,点D为边AC的中点,点E为边AB上离点A较近的三等分点,则
如图,已知正三角形ABC的边长为2,点D为边AC的中点,点E为边AB上离点A较近的三等分点,则