题目内容
（2012•黑龙江）已知正三角形ABC的顶点A（1，1），B（1，3），顶点C在第一象限，若点（x，y）在△ABC内部，则z=-x+y的取值范围是（ ）
分析：由A，B及△ABC为正三角形可得，可求C的坐标，然后把三角形的各顶点代入可求z的值，进而判断最大与最小值，即可求解范围
解答：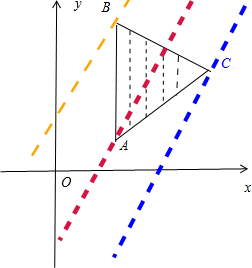
解：设C（a，b），（a＞0，b＞0）
由A（1，1），B（1，3），及△ABC为正三角形可得，AB=AC=BC=2
即（a-1）2+（b-1）2=（a-1）2+（b-3）2=4
∴b=2，a=1+
即C（1+
，2）
则此时直线AB的方程x=1，AC的方程为y-1=
（x-1），直线BC的方程为y-3=（
-2）（x-1）
当直线x-y+z=0经过点A（1，1）时，z=0，经过点B（1，3）z=2，经过点C（1+
，2）时，z=1-
∴zmax=2，zmin=1-
故选A
解：设C（a，b），（a＞0，b＞0）由A（1，1），B（1，3），及△ABC为正三角形可得，AB=AC=BC=2
即（a-1）2+（b-1）2=（a-1）2+（b-3）2=4
∴b=2，a=1+
| 3 |
| 3 |
则此时直线AB的方程x=1，AC的方程为y-1=
| ||
| 3 |
| 3 |
当直线x-y+z=0经过点A（1，1）时，z=0，经过点B（1，3）z=2，经过点C（1+
| 3 |
| 3 |
∴zmax=2，zmin=1-
| 3 |
故选A
点评：考查学生线性规划的理解和认识，考查学生的数形结合思想．属于基本题型．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目