题目内容
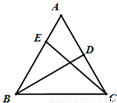
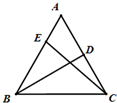 如图,已知正三角形ABC的边长为2,点D为边AC的中点,点E为边AB上离点A较近的三等分点,则
如图,已知正三角形ABC的边长为2,点D为边AC的中点,点E为边AB上离点A较近的三等分点,则| BD |
| CE |
-1
-1
.分析:由题意选基向量,再由向量的加减法和数乘几何意义,用基向量表示出
和
,再由数量积的运算求出式子的值.
| BD |
| CE |
解答:解:由题意选基向量
和
,且|
|=|
|=2,它们的夹角为60°,
∴
=
-
=
-
,
=
-
=
-
,
∴
•
=(
-
)•(
-
)
=
•
-
2-
2+
•
=
•
-
2-
2
=
×2×2×
-
×4-
×4=-1,
故答案为:-1.
| AB |
| AC |
| AB |
| AC |
∴
| BD |
| AD |
| AB |
| 1 |
| 2 |
| AC |
| AB |
| CE |
| AE |
| AC |
| 1 |
| 3 |
| AB |
| AC |
∴
| BD |
| CE |
| 1 |
| 2 |
| AC |
| AB |
| 1 |
| 3 |
| AB |
| AC |
=
| 1 |
| 6 |
| AC |
| AB |
| 1 |
| 2 |
| AC |
| 1 |
| 3 |
| AB |
| AB |
| AC |
=
| 7 |
| 6 |
| AC |
| AB |
| 1 |
| 2 |
| AC |
| 1 |
| 3 |
| AB |
=
| 7 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
故答案为:-1.
点评:本题考查向量数量积在几何中的应用,以及向量的加减法和数乘几何意义,解答关键是选基向量和利用向量数量积的运算性质,属于中档题.

练习册系列答案
相关题目
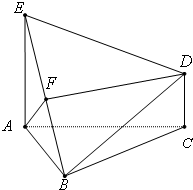 20、如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点.
20、如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点.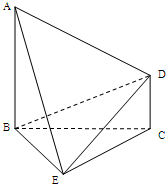 如图,已知AB⊥平面BCE,CD∥ab,△BCE是正三角形,AB=BC=2CD.
如图,已知AB⊥平面BCE,CD∥ab,△BCE是正三角形,AB=BC=2CD.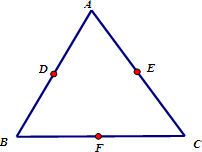 (2012•江苏一模)如图,已知面积为1的正三角形ABC三边的中点分别为D、E、F,从A,B,C,D,E,F六个点中任取三个不同的点,所构成的三角形的面积为X(三点共线时,规定X=0)
(2012•江苏一模)如图,已知面积为1的正三角形ABC三边的中点分别为D、E、F,从A,B,C,D,E,F六个点中任取三个不同的点,所构成的三角形的面积为X(三点共线时,规定X=0)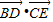 = .
= .