题目内容
设椭圆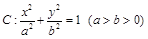 的左、右焦点分别为
的左、右焦点分别为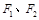 ,上顶点为
,上顶点为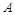 ,离心率为
,离心率为 ,在
,在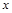 轴负半轴上有一点
轴负半轴上有一点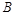 ,且
,且
(1)若过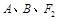 三点的圆恰好与直线
三点的圆恰好与直线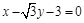 相切,求椭圆C的方程;
相切,求椭圆C的方程;
(2)在(1)的条件下,过右焦点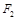 作斜率为
作斜率为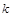 的直线
的直线 与椭圆C交于
与椭圆C交于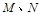 两点,在
两点,在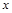 轴上是否存在点
轴上是否存在点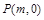 ,使得以
,使得以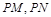 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出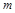 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由.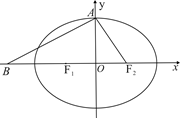
1)由题意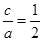 ,得
,得
 ,所以
,所以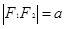
又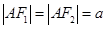 由于
由于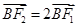 ,所以
,所以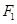 为
为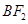 的中点,
的中点,
所以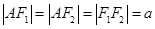
所以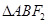 的外接圆圆心为
的外接圆圆心为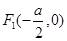 ,半径
,半径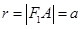 …………………3分
…………………3分
又过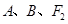 三点的圆与直线
三点的圆与直线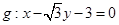 相切,
相切,
所以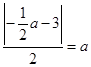 解得
解得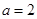 ,
,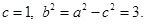
所求椭圆方程为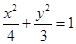 …………………………………………………… 6分
…………………………………………………… 6分
(2)有(1)知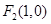 ,设
,设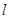 的方程为:
的方程为: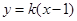
将直线方程与椭圆方程联立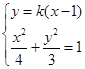 ,整理得
,整理得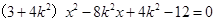
设交点为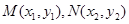 ,因为
,因为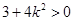
则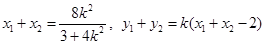 ……………………………………8分
……………………………………8分
若存在点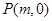 ,使得以
,使得以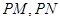 为邻边的平行四边形是菱形,
为邻边的平行四边形是菱形,
由于菱形对角线垂直,所以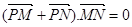
又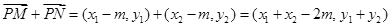
又 的方向向量是
的方向向量是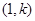 ,故
,故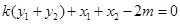 ,则
,则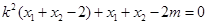 ,即
,即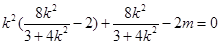
由已知条件知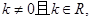
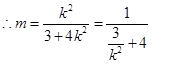 ………………………11分
………………………11分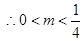 ,故存在满足题意的点
,故存在满足题意的点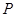 且
且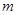 的取值范围是
的取值范围是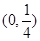
解析

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 、B
、B 、C
、C 三点,过坐标原点O的直线
三点,过坐标原点O的直线 与抛物线交于M、N两点.分别过点C、D
与抛物线交于M、N两点.分别过点C、D 作平行于
作平行于 轴的直线
轴的直线 、
、 .(1)求抛物线对应的二次函数的解析式;(2)求证:以ON为直径的圆与直线
.(1)求抛物线对应的二次函数的解析式;(2)求证:以ON为直径的圆与直线 表示),并证明M、N两点到直线
表示),并证明M、N两点到直线
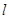 与椭圆
与椭圆 交于
交于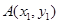 ,
,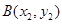 两点,已知
两点,已知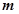
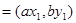 ,
,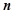
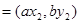 ,若
,若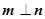 且椭圆的离心率
且椭圆的离心率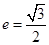 ,又椭圆经过点
,又椭圆经过点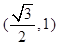 ,
,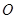 为坐标原点.
为坐标原点.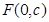 (
(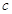 为半焦距),求直线
为半焦距),求直线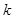 的值;
的值;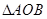 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.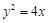 ,点
,点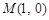 关于
关于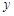 轴的对称点为
轴的对称点为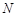 ,直线
,直线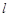 过点
过点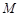 交抛物线于
交抛物线于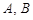 两点.
两点.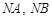 的斜率互为相反数;
的斜率互为相反数; 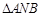 面积的最小值;
面积的最小值;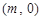 ,
,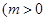 且
且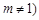 .根据(1)(2)推测并回答下列问题(不必说明理由):①直线
.根据(1)(2)推测并回答下列问题(不必说明理由):①直线
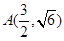 是曲线C1和C2的交点.
是曲线C1和C2的交点.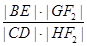 是否为定值,若是,求出定值;若不是,请说明理由.
是否为定值,若是,求出定值;若不是,请说明理由.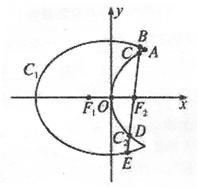

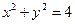 上任取一点
上任取一点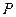 ,过点
,过点 轴的垂线段
轴的垂线段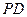 ,
,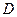 为垂足.当点
为垂足.当点 形成轨迹
形成轨迹 .
.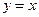 与曲线
与曲线 两点,
两点,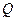 为曲线
为曲线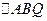 面积的最大值
面积的最大值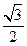 的椭圆
的椭圆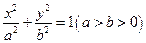 上的点到
上的点到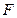 的最长距离为
的最长距离为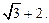
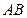 ,若点
,若点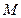 在
在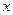 轴上,且使得
轴上,且使得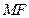 为
为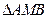 的一条内角平分线,则称点
的一条内角平分线,则称点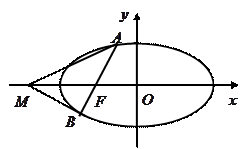
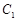 是以原点O为中心、
是以原点O为中心、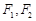 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线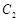 是以O为顶点、
是以O为顶点、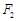 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线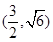 且
且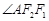 为钝角.
为钝角. 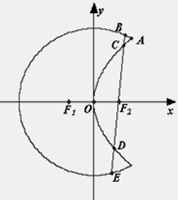
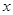 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线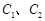 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问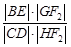 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由.