题目内容
【题目】已知函数f(x)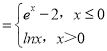 ,g(x)=f(
,g(x)=f(![]() )+1(k∈R,k≠0),则下列关于函数y=f[g(x)]+1的零点个数判断正确的是( )
)+1(k∈R,k≠0),则下列关于函数y=f[g(x)]+1的零点个数判断正确的是( )
A.当k>0时,有2个零点;当k<0时,有4个零点
B.当k>0时,有4个零点;当k<0时,有2个零点
C.无论k为何值,均有2个零点
D.无论k为何值,均有4个零点
【答案】B
【解析】
根据方程的跟和函数的零点的关系,将函数![]() 的零点个数转化为
的零点个数转化为![]() 和
和![]() 以及
以及![]() 的交点,即可求解.
的交点,即可求解.
依题意,当x=0或x![]() 时,f(x)=﹣1,
时,f(x)=﹣1,
函数y=f[g(x)]+1的零点个数,即为方程f[g(x)]=﹣1的解的个数,
即为方程g(x)=0或g(x)![]() 的解的个数,
的解的个数,
即为方程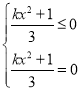 或者
或者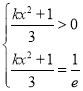 或
或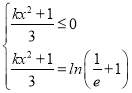 (舍去)
(舍去)
或者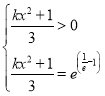 解的个数,
解的个数,
即为![]() 0或者
0或者![]() 或者
或者![]() 解的个数,
解的个数,
由![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
①当k>0时,y![]() 为顶点为(0,
为顶点为(0,![]() ),开口向上的抛物线,y
),开口向上的抛物线,y![]() 与y
与y![]() 和
和![]() 分别有两个交点,与y=0无交点,
分别有两个交点,与y=0无交点,
故当k>0时,函数y=f[g(x)]+1有4个零点;
②当k<0时,y![]() 为顶点为(0,
为顶点为(0,![]() ),开口向下的抛物线,y
),开口向下的抛物线,y![]() 与y=0有两个交点,与y
与y=0有两个交点,与y![]() 和
和![]() 无交点,
无交点,
故当k<0时,函数y=f[g(x)]+1有2个零点;
综上,当k>0时,有4个零点;当k<0时,有2个零点,
故选:B.

【题目】某调查机构为了解人们对某个产品的使用情况是否与性别有关,在网上进行了问卷调查,在调查结果中随机抽取了![]() 份进行统计,得到如下
份进行统计,得到如下![]() 列联表:
列联表:
男性 | 女性 | 合计 | |
使用 | 15 | 5 | 20 |
不使用 | 10 | 20 | 30 |
合计 | 25 | 25 | 50 |
(1)请根据调查结果你有多大把握认为使用该产品与性别有关;
(2)在不使用该产品的人中,按性别用分层抽样抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人参加某项活动,记被抽中参加该项活动的女性人数为
人参加某项活动,记被抽中参加该项活动的女性人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附: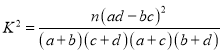 ,
,
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
【题目】某水果种植基地引进一种新水果品种,经研究发现该水果每株的产量![]() (单位:
(单位:![]() )和与它“相近”的株数
)和与它“相近”的株数![]() 具有线性相关关系(两株作物“相近”是指它们的直线距离不超过
具有线性相关关系(两株作物“相近”是指它们的直线距离不超过![]() ),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
(1)求出该种水果每株的产量![]() 关于它“相近”株数
关于它“相近”株数![]() 的回归方程;
的回归方程;
(2)有一种植户准备种植该种水果500株,且每株与它“相近”的株数都为![]() ,计划收获后能全部售出,价格为10元
,计划收获后能全部售出,价格为10元![]() ,如果收入(收入=产量×价格)不低于25000元,则
,如果收入(收入=产量×价格)不低于25000元,则![]() 的最大值是多少?
的最大值是多少?
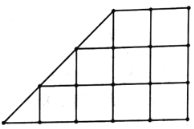
(3)该种植基地在如图所示的直角梯形地块的每个交叉点(直线的交点)处都种了一株该种水果,其中每个小正方形的边长和直角三角形的直角边长都为![]() ,已知该梯形地块周边无其他树木影响,若从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的分布列与数学期望.
,已知该梯形地块周边无其他树木影响,若从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的分布列与数学期望.
附:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: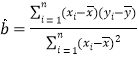 ,
,![]() .
.