题目内容
【题目】如图,在三棱锥P﹣ABC中,AC=![]() BC,AB=2BC,D为线段AB上一点,且AD=3DB,PD⊥平面ABC,PA与平面ABC所成的角为45°.
BC,AB=2BC,D为线段AB上一点,且AD=3DB,PD⊥平面ABC,PA与平面ABC所成的角为45°.
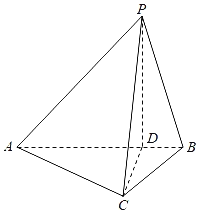
(1)求证:平面PAB⊥平面PCD;
(2)求二面角P﹣AC﹣D的平面角的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)推导出AC⊥BC,CD⊥AD,PD⊥CD,从而CD⊥平面PAB,由此能证明平面PAB⊥平面PCD.
(2)以D为坐标原点,分别以DC,DB,DP所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角P-AC-D的平面角的余弦值.
(1)证明:∵AC=![]() BC,AB=2BC,
BC,AB=2BC,
∴![]() ,
,
∴AB2=AC2+BC2,∴AC⊥BC,
在Rt△ABC中,由AC=![]() BC,得∠CAB=30°,
BC,得∠CAB=30°,
设BD=1,由AD=3BD,得AD=3,BC=2,AC=2![]() ,
,
在△ACD中,由余弦定理得CD2=AD2+AC2﹣2ADACcos30°=3,
∴CD=![]() ,
,
∴CD2+AD2=AC2,∴CD⊥AD,
∵PD⊥平面ABC,CD![]() 平面ABC,
平面ABC,
∴PD⊥CD,
又PD∩AD=D,∴CD⊥平面PAB,
又CD![]() 平面PCD,∴平面PAB⊥平面PCD.
平面PCD,∴平面PAB⊥平面PCD.
(2)解:∵PD⊥平面ABC,
∴PA与平面ABC所成角为∠PAD,即∠PAD=45°,
∴△PAD为等腰直角三角形,PD=AD,
由(1)得PD=AD=3,以D为坐标原点,
分别以DC,DB,DP所在直线为x,y,z轴,建立空间直角坐标系,

则D(0,0,0),C(![]() ,0,0),A(0,﹣3,0),P(0,0,3),
,0,0),A(0,﹣3,0),P(0,0,3),
![]() =(0,﹣3,﹣3),
=(0,﹣3,﹣3),![]() =(
=(![]() ),
),
则![]() =(0,0,3)是平面ACD的一个法向量,
=(0,0,3)是平面ACD的一个法向量,
设平面PAC的一个法向量![]() =(x,y,z),
=(x,y,z),
则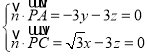 ,取x=
,取x=![]() ,得
,得![]() =(
=(![]() ,﹣1,1),
,﹣1,1),
设二面角P﹣AC﹣D的平面角为θ,
则cosθ=![]() =
=![]() ,
,
∴二面角P﹣AC﹣D的平面角的余弦值为![]() .
.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案【题目】高铁是一种快捷的交通工具,为我们的出行提供了极大的方便。某高铁换乘站设有编号为①,②,③,④,⑤的五个安全出口,若同时开放其中的两个安全出口,疏散![]() 名乘客所需的时间如下:
名乘客所需的时间如下:
安全出口编号 | ①② | ②③ | ③④ | ④⑤ | ①⑤ |
疏散乘客时间(s) | 120 | 220 | 160 | 140 | 200 |
则疏散乘客最快的一个安全出口的编号是( )
A. ①B. ②C. ④D. ⑤