题目内容
若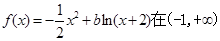 上是减函数,则
上是减函数,则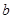 的最大值是
的最大值是
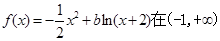 上是减函数,则
上是减函数,则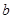 的最大值是
的最大值是 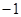
试题分析:函数的定义域是
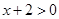 ,即
,即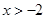 ,而
,而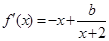 ,令
,令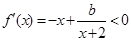 ,得
,得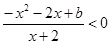 ,因为
,因为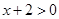 ,所以
,所以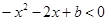 ,函数
,函数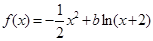 在
在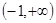 上是减函数,即
上是减函数,即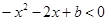 在
在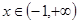 恒成立,得
恒成立,得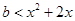 在
在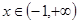 恒成立,令
恒成立,令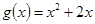 ,即只要
,即只要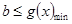 即可,而
即可,而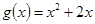 在
在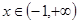 的最小值
的最小值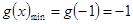 ,所以
,所以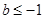 。
。
练习册系列答案
相关题目
题目内容
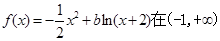 上是减函数,则
上是减函数,则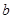 的最大值是
的最大值是 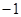
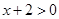 ,即
,即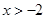 ,而
,而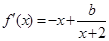 ,令
,令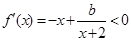 ,得
,得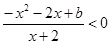 ,因为
,因为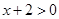 ,所以
,所以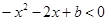 ,函数
,函数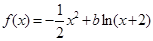 在
在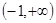 上是减函数,即
上是减函数,即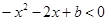 在
在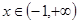 恒成立,得
恒成立,得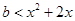 在
在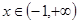 恒成立,令
恒成立,令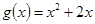 ,即只要
,即只要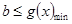 即可,而
即可,而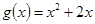 在
在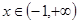 的最小值
的最小值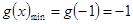 ,所以
,所以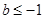 。
。