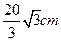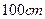题目内容
(本小题满分12分)
设函数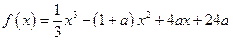 ,其中常数
,其中常数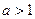
(Ⅰ)讨论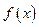 的单调性;
的单调性;
(Ⅱ)若当x≥0时,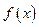 >0恒成立,求
>0恒成立,求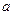 的取值范围.
的取值范围.
设函数
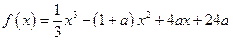 ,其中常数
,其中常数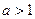
(Ⅰ)讨论
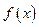 的单调性;
的单调性;(Ⅱ)若当x≥0时,
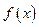 >0恒成立,求
>0恒成立,求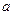 的取值范围.
的取值范围.:(I)
由 知,当
知,当 时,
时, ,故
,故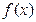 在区间
在区间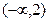 是增函数;
是增函数;
当 时,
时, ,故
,故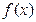 在区间
在区间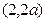 是减函数;
是减函数;
当 时,
时, ,故
,故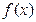 在区间
在区间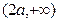 是增函数.
是增函数.
综上,当 时,
时,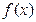 在区间
在区间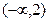 和
和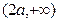 是增函数,在区间
是增函数,在区间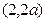 是减函数.
是减函数.
(II)由(I)知,当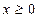 时,
时,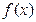 在
在 或
或 处取得最小值.
处取得最小值.


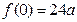
由假设知
 即
即 解得
解得
故 的取值范围是(1,6)
的取值范围是(1,6) 


由
 知,当
知,当 时,
时, ,故
,故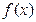 在区间
在区间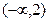 是增函数;
是增函数;当
 时,
时, ,故
,故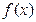 在区间
在区间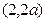 是减函数;
是减函数;当
 时,
时, ,故
,故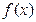 在区间
在区间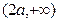 是增函数.
是增函数.综上,当
 时,
时,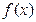 在区间
在区间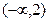 和
和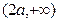 是增函数,在区间
是增函数,在区间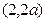 是减函数.
是减函数.(II)由(I)知,当
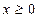 时,
时,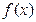 在
在 或
或 处取得最小值.
处取得最小值.

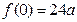
由假设知
 即
即 解得
解得
故
 的取值范围是(1,6)
的取值范围是(1,6) 

:因为第(Ⅰ)题中要求函数的单调区间,利用导数的正负即可求出,所以首先要求出函数的导数,然后解不等式 和
和 即可. 第(Ⅱ)小题是一个恒成立问题,转化为求函数的最值解决,所以要求出函数
即可. 第(Ⅱ)小题是一个恒成立问题,转化为求函数的最值解决,所以要求出函数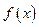 在x≥0时的最小值.
在x≥0时的最小值.
 和
和 即可. 第(Ⅱ)小题是一个恒成立问题,转化为求函数的最值解决,所以要求出函数
即可. 第(Ⅱ)小题是一个恒成立问题,转化为求函数的最值解决,所以要求出函数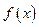 在x≥0时的最小值.
在x≥0时的最小值.
练习册系列答案
相关题目
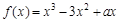
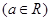 .
.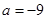 时,求函数
时,求函数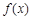 的极大值;
的极大值;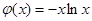 的图象有三个不同的交点,求
的图象有三个不同的交点,求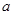 的取值范围;
的取值范围;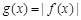 ,当
,当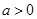 时,求函数
时,求函数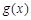 的单调减区间.
的单调减区间.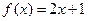 在区间
在区间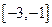 上的平均变化率为
上的平均变化率为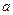 ,在区间
,在区间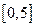 上的平均变化率为
上的平均变化率为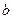 ,则下列结论中正确的是( )
,则下列结论中正确的是( )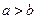
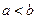
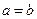
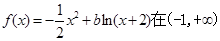 上是减函数,则
上是减函数,则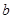 的最大值是
的最大值是 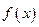 为可导函数,且满足
为可导函数,且满足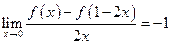 ,则过曲线
,则过曲线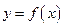 上点
上点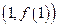 处的切线率为
处的切线率为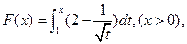 则
则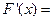 ______.
______.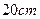 ,要使其体积为最大,则其高为多少厘米( )
,要使其体积为最大,则其高为多少厘米( )