题目内容
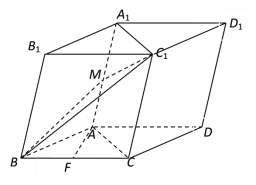
【题目】已知四边形ABCD满足AD∥BC,BA=AD=DC=![]() BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.
BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.
(1)证明:B1E∥平面ACF;
(2)求平面ADB1与平面ECB1所成锐二面角的余弦值.
【答案】证明:(1)连结ED交AC于O,连结OF,
因为AECD为菱形,OE=OD,
所以FO∥B1E,
所以B1E∥平面ACF.
(2)取AE的中点M,连结B1M,连结MD,则∠AMD=90°,
分别以ME,MD,MB1为x,y,z轴建系,
则E(![]() ,0,0),C(a,
,0,0),C(a,![]() a,0),A(﹣
a,0),A(﹣![]() ,0,0),D(0,
,0,0),D(0,![]() a,0),
a,0),
B1(0,0,![]() a),
a),
则![]() =(﹣
=(﹣![]() ,0,
,0,![]() a),
a),![]() =(
=(![]() ,
,![]() a,0),
a,0),![]() =(
=(![]() ,0,
,0,![]() a),
a),
设面ECB1的法向量为![]() =(x,y,z),
=(x,y,z),
则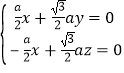 ,令x=1,则
,令x=1,则![]() =(1,﹣
=(1,﹣![]() ,
,![]() ),
),
同理面ADB1的法向量为![]() =(1,﹣
=(1,﹣![]() ,﹣
,﹣![]() )
)
所以cos<![]() ,
,![]() >=
>=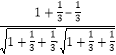 =
=![]() ,
,
故平面ADB1与平面ECB1所成锐二面角的余弦值为![]()
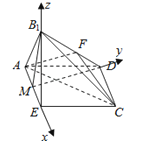
【解析】(1)根据线面平行的判定定理即可证明:B1E∥平面ACF;
(2)建立空间坐标系,求出平面的法向量,利用向量法即可得到结论.
【考点精析】通过灵活运用直线与平面平行的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行即可以解答此题.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案【题目】辽宁号航母纪念章从2012年10月5日起开始上市,通过市场调查,得到该纪念章每![]() 枚的市场价
枚的市场价![]() (单位:元)与上市时间
(单位:元)与上市时间![]() (单位:天)的数据如下:
(单位:天)的数据如下:
上市时间 |
|
|
|
市场价 |
|
|
|
(1)根据上表数据,从下列函数中选取一个恰当的函数描述辽宁号航母纪念章的市场价![]() 与上市时间
与上市时间![]() 的变化关系:①
的变化关系:①![]() ;②
;②![]() ;③
;③![]() ;
;
(2)利用你选取的函数,求辽宁号航母纪念章市场价最低时的上市天数及最低的价格;
(3)设你选取的函数为![]() ,若对任意实数
,若对任意实数![]() ,关于
,关于![]() 的方程
的方程![]() 恒有个想异实数根,求
恒有个想异实数根,求![]() 的取值范围.
的取值范围.