Question

【题目】已知函数其图像的一个对称中心是将的图像向左平移个单位长度后得到函数的图像。

(1)求函数的解析式；

(2)若对任意当时，都有求实数的最大值；

(3)若对任意实数在上与直线的交点个数不少于6个且不多于10个，求正实数的取值范围。

Answer 1

【答案】（1） ； （2）； （3）.

【解析】

（1）由图像的一个对称中心是列方程即可求得，即可求得，利用平移规律得，问题得解。

（2）由题可得在上单调递增，求得的增区间为，利用即可求得，问题得解。

（3）的最小正周期为，由题可得：的区间长度满足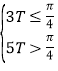，解不等式即可。

（1）由题意，得，

解得，

又，∴，

∴，

从而 ；

（2）对任意，且，

，

即在上单调递增，

，

易得其单调增区间为，由于，

∴当时，，从而，∴实数的最大值为；

（3），其最小正周期为，而区间的长度为，

要满足题意，则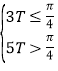，∴，解得.