题目内容
(本题满分20分)
设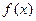 是定义在实数
是定义在实数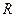 上的函数,
上的函数,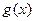 是定义在正整数
是定义在正整数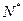 上的函数,同时满足下列条件:
上的函数,同时满足下列条件:
(1)任意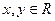 ,有
,有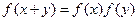 ,当
,当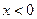 时,
时,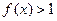 且
且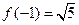 ;
;
(2)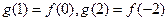 ;
;
(3)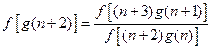 ,
,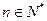
试求:(1)证明:任意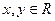 ,
,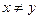 ,都有
,都有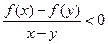 ;
;
(2)是否存在正整数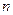 ,使得
,使得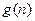 是25的倍数,若存在,求出所有自然数
是25的倍数,若存在,求出所有自然数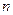 ;若不存在说明理由.(阶乘定义:
;若不存在说明理由.(阶乘定义: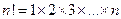 )
)
设
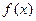 是定义在实数
是定义在实数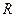 上的函数,
上的函数,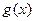 是定义在正整数
是定义在正整数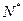 上的函数,同时满足下列条件:
上的函数,同时满足下列条件:(1)任意
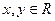 ,有
,有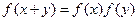 ,当
,当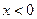 时,
时,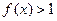 且
且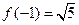 ;
;(2)
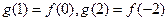 ;
;(3)
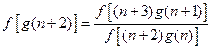 ,
,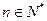
试求:(1)证明:任意
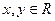 ,
,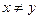 ,都有
,都有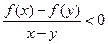 ;
;(2)是否存在正整数
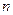 ,使得
,使得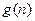 是25的倍数,若存在,求出所有自然数
是25的倍数,若存在,求出所有自然数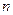 ;若不存在说明理由.(阶乘定义:
;若不存在说明理由.(阶乘定义: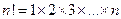 )
)解:(1)当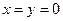 时,
时,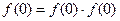 ,
,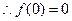 ,
,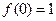
若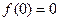 ,则得
,则得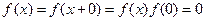 ,不可能,舍去
,不可能,舍去 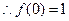
当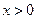 时,
时,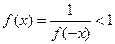 ,得,
,得,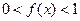
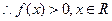
若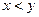 ,则,
,则,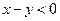 ,
,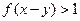 ,
,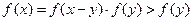 ,
,
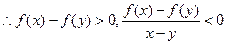
同理,若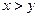 ,
,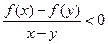
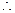 任意
任意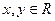 ,
,
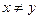 ,都有
,都有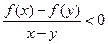
(2)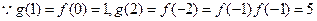
由(1)可得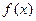 为单调减函数
为单调减函数
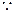
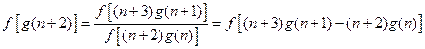
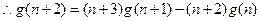
得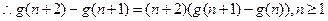

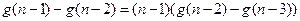
…
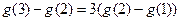
相乘得: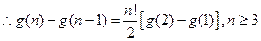 …①
…①
又由①式得: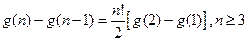
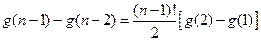
…
 ,
,
相加得: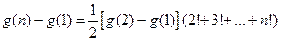 ,
,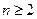

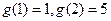 ,
,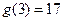 ,
,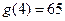 ,
,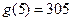 ,
,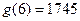 ,
,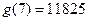 ,
,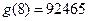 ,
,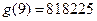 ,
,
由于当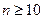 时,
时,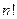 能被25整除
能被25整除
综上,存在正整数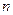 ,当
,当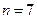 或
或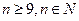 时,
时,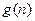 是25的倍数
是25的倍数
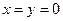 时,
时,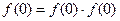 ,
,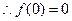 ,
,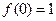
若
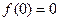 ,则得
,则得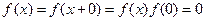 ,不可能,舍去
,不可能,舍去 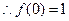
当
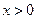 时,
时,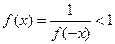 ,得,
,得,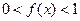
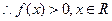
若
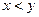 ,则,
,则,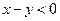 ,
,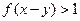 ,
,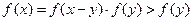 ,
,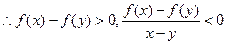
同理,若
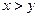 ,
,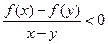
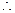 任意
任意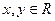 ,
,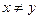 ,都有
,都有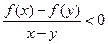
(2)
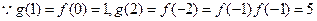
由(1)可得
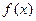 为单调减函数
为单调减函数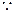
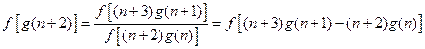
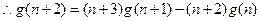
得
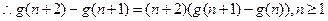

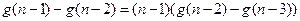
…
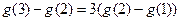
相乘得:
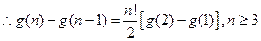 …①
…① 又由①式得:
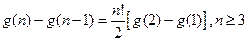
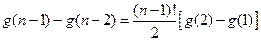
…
 ,
,
相加得:
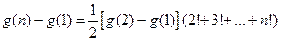 ,
,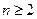

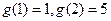 ,
,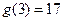 ,
,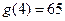 ,
,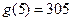 ,
,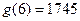 ,
,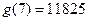 ,
,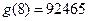 ,
,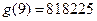 ,
,由于当
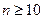 时,
时,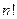 能被25整除
能被25整除综上,存在正整数
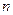 ,当
,当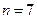 或
或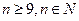 时,
时,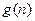 是25的倍数
是25的倍数
练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
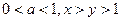 ,则下列关系式中正确的个数是 ( )
,则下列关系式中正确的个数是 ( )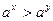 ②
②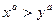
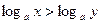 ④
④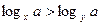
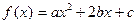 ,其中a≥b>c,a+b+c=0.
,其中a≥b>c,a+b+c=0.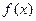 有两个零点;
有两个零点;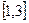 上的最小值为1,最大值为13,求a、b、c的值.
上的最小值为1,最大值为13,求a、b、c的值.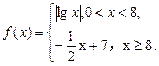 ,若
,若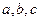 互不相等,且
互不相等,且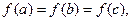 则
则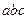 的取值范围是 .
的取值范围是 .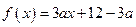 在
在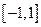 上存在
上存在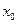 ,使
,使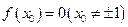 ,则
,则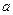 的取值范围是
的取值范围是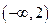


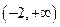
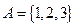 ,集合
,集合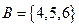 ,在
,在 的映射中满足1的象是4的有( )
的映射中满足1的象是4的有( )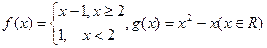 ,则方程
,则方程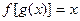 的解为 .
的解为 .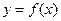 为区间
为区间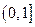 上的图像是连续不断的一条曲线,且恒有
上的图像是连续不断的一条曲线,且恒有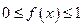 ,可以用随机模拟方法计算由曲线
,可以用随机模拟方法计算由曲线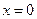 ,
,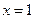 ,
,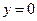 所围成部分的面积,先产生两组
所围成部分的面积,先产生两组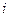 每组
每组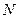 个,区间
个,区间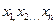 和
和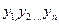 ,由此得到V个点
,由此得到V个点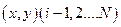 。再数出其中满足
。再数出其中满足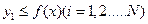 的点数
的点数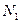 ,那么由随机模拟方法可得S的近似值为___________
,那么由随机模拟方法可得S的近似值为___________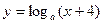 ,明文
,明文 密文
密文 密文
密文 明文.如上所示,明文“4”通过加密加密后得到“3”再发送,接受方通过解密钥解密得明文“4”,问若接受方接到密文为“4”,则解密后得明文是______________________.
明文.如上所示,明文“4”通过加密加密后得到“3”再发送,接受方通过解密钥解密得明文“4”,问若接受方接到密文为“4”,则解密后得明文是______________________.