题目内容

设（
2
-x）10=a0+a1x+a2x2+…+a10x10，求（a0+a2+…+a10）2（a1+a3+…+a9）2的值．
令x=1可得：a0+a1+a2+…+a10=(
2
-1)10，再令x=-1可得 a0-a1+a2-a3+…+a8-a9+a10=(
2
+1)10．
由以上两式可得 a0+a2+…+a10 =
(
2
-1)10+(
2
+1)10
2
，a1+a3+…+a9=
(
2
-1)10-(
2
+1)10
2
，
∴（a0+a2+…+a10）2 =
(
2
-1)20+(
2
+1)20+2
4
，（a1+a3…+a9）2=
(
2
-1)20+(
2
+1)20-2
4
，
∴（a0+a2+…+a10）2（a1+a3+…+a9）2 =
(
2
-1)20+(
2
+1)20+2
4
-
(
2
-1)20+(
2
+1)20-2
4
=1．
练习册系列答案
相关题目
已知(1+2
x
)n的展开式中，某一项的系数是它前一项系数的2倍，而等于它后一项的系数的
5
6
．
（1）求该展开式中二项式系数最大的项；
（2）求展开式中系数最大的项．
若（1+2x）100=a0+a1（x-1）+…+a100（x-1）100，则a1+a2+…+a100=（　　）
A．5100-3100B．5100C．3100D．3100-1
已知a=2
∫π0
cos(x+
π
6
)dx，则二项式(x2+
a
x
)10的展开式中二项式系数最大项为______．
若（1+x）4=a0+a1x+a2x2+a3x3+a4x4，则a1+a3的值为______．
（1）求(
1
x
-
x
2
)9的展开式中的常数项；
（2）已知x10=a0+a1(x+2)+a2(x+2)2+…a10(x+2)10，求a1+a2+a3+…a10的值．
(2x3-
1
2x
)7的展开式中系数为有理数的项的个数是（　　）
A．5B．4C．3D．2
式子-2Cn1+4Cn2-8Cn3+…+（-2）nCnn等于（　　）
A．（-1）nB．（-1）n-1C．3nD．3n-1
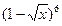的展开式中x的系数为           

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网