题目内容

若（1+2x）100=a0+a1（x-1）+…+a100（x-1）100，则a1+a2+…+a100=（　　）
A．5100-3100B．5100C．3100D．3100-1
在（1+2x）100=a0+a1（x-1）+…+a100（x-1）100 中，令x=1，可得 a0=3100．
再令x=2，可得a0+a1+a2+…+a100=5100，∴a1+a2+…+a100=5100-3100，
故选A．
练习册系列答案
相关题目
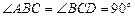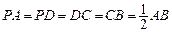（12分）如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD, ，，E是BD的中点．
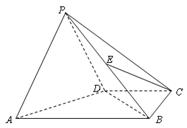  （1）求证：EC//平面APD；
（2）求BP与平面ABCD所成角的正切值；
（3） 求二面角P-AB-D的大小．
若（23-7）7=a737+a636+…+a73+a大，则a7+a1+a3+a7=______．
如果（3a-
1
3a2
）n的展开式中各项系数之和为128，则展开式中a2的系数是（　　）
A．-2835B．2835C．21D．-21
设（
2
-x）10=a0+a1x+a2x2+…+a10x10，求（a0+a2+…+a10）2（a1+a3+…+a9）2的值．
若（2x-1）11=a0+a1x+a2x2+…+a11x11，则a0+a1+a2+…+a11=______．
已知（
a
+
1
3a2
)n的展开式的第三项与第二项的系数的比为11：2，则n是（　　）
A．10B．11C．12D．13
(
x
-
3
x
)n的展开式中各项二项式系数的和为64，则该展开式中的常数项为______．
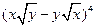的展开式中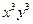的系数为          .

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网