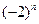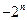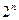题目内容

若（1+x）4=a0+a1x+a2x2+a3x3+a4x4，则a1+a3的值为______．
∵（1+x）4=a0+a1x+a2x2+a3x3+a4x4，
∴当x=-1时，0=a0-a1+a2-a3+a4①
当x=1时，24=a0+a1+a2+a3+a4②
②-①得2（a1+a3）=24
∴a1+a3=8
故答案为：8
练习册系列答案
相关题目
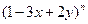
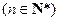的展开式中不含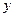的项的系数之和为（）
A．B．C．D．1
若（23-7）7=a737+a636+…+a73+a大，则a7+a1+a3+a7=______．
设（
2
-x）10=a0+a1x+a2x2+…+a10x10，求（a0+a2+…+a10）2（a1+a3+…+a9）2的值．
若（2x-1）11=a0+a1x+a2x2+…+a11x11，则a0+a1+a2+…+a11=______．
设(5x-
1
x
)n的展开式的各项系数之和为M，二项式系数之和为N，若
M
N
=32，则展开式中x2的系数为______．
已知（
a
+
1
3a2
)n的展开式的第三项与第二项的系数的比为11：2，则n是（　　）
A．10B．11C．12D．13
在（
3x
+
1
x
）20的展开式中，x的幂指数是整数的项共有（　　）
A．3项B．4项C．5项D．6项
已知(
x
-
2
x2
)n（n∈N*）展开式中二项式系数和为256．
（1）此展开式中有没有常数项？有理项的个数是几个？并说明理由．
（2）求展开式中系数最小的项．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网