题目内容
已知(1+2
)n的展开式中,某一项的系数是它前一项系数的2倍,而等于它后一项的系数的
.
(1)求该展开式中二项式系数最大的项;
(2)求展开式中系数最大的项.
| x |
| 5 |
| 6 |
(1)求该展开式中二项式系数最大的项;
(2)求展开式中系数最大的项.
(1)第r+1项系数为Cnr•2r,第r项系数为Cnr-1•2r-1,第r+2项系数为Cnr+1•2r+1
依题意得到
,即
,解得n=7,
所以二项式系数最大的项是第4项和第5项.
所以T4=
(2
)3=280x
,T5=
(2
)4=560x2.
(2)设第r+1项的系数最大,则
解得
≤r≤
又因为r∈N,所以r=5
∴展开式中系数最大的项为T6=
(2
)5=672•x
依题意得到
|
|
所以二项式系数最大的项是第4项和第5项.
所以T4=
| C | 37 |
| x |
| 5 |
| 2 |
| C | 47 |
| x |
(2)设第r+1项的系数最大,则
|
解得
| 13 |
| 3 |
| 16 |
| 3 |
又因为r∈N,所以r=5
∴展开式中系数最大的项为T6=
| C | 57 |
| x |
| 5 |
| 2 |

练习册系列答案
相关题目
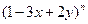
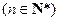 的展开式中不含
的展开式中不含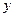 的项的系数之和为()
的项的系数之和为()
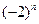
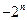
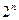
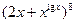 的展开式中,二项式系数最大的项的值等于
的展开式中,二项式系数最大的项的值等于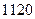 ,求
,求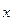 .
. )9展开式中x2的系数是 .(用数字作答)
)9展开式中x2的系数是 .(用数字作答)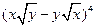 的展开式中
的展开式中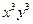 的系数为 .
的系数为 .