题目内容
(本小题满分12分)
已知数列 的前
的前 项和为
项和为 ,对一切正整数
,对一切正整数 ,点
,点 都在函数
都在函数 的图像上.
的图像上.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的通项公式.
的通项公式.
已知数列
 的前
的前 项和为
项和为 ,对一切正整数
,对一切正整数 ,点
,点 都在函数
都在函数 的图像上.
的图像上.(Ⅰ)求数列
 的通项公式;
的通项公式;(Ⅱ)设
 ,求数列
,求数列 的通项公式.
的通项公式.(1) 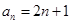 (2)
(2) 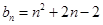
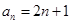 (2)
(2) 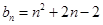
试题分析:解:
⑴由已知
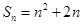
∴n≥2时,
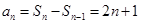 ………………5分
………………5分又
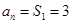 满足上式
满足上式∴
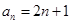 ………………………………6分
………………………………6分⑵由
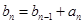
∴
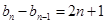 ……………………7分
……………………7分∴

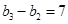
……
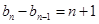 …………………………9分
…………………………9分累加可得
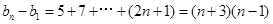
∴
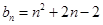 ……………………11分
……………………11分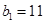 满足上式
满足上式∴
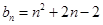 ………………………………12分
………………………………12分点评:解决该试题的关键是利用通项公式与前n项和的关系式来求解通项公式,同时还利用递推关系式,采用累加法 的思想来求解数列的通项公式,属于中档题,考查了同学们不同的角度来处理相应问题的能力运用。

练习册系列答案
相关题目
 的前
的前 项和记为
项和记为
 的各项为正,其前
的各项为正,其前 ,且
,且 ,又
,又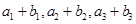 成等比数列,求
成等比数列,求 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且 成等比数列.
成等比数列. ,求数列
,求数列 的前
的前 项和
项和
 分别在射线
分别在射线 (不含端点
(不含端点 )上运动,
)上运动, ,在
,在 中,角
中,角 、
、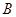 、
、 、
、 、
、 .
.
 ,
, ,试用
,试用 表示
表示 中,若
中,若 ,则该数列前2013项的和为
,则该数列前2013项的和为
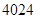


 和
和 满足
满足 ,
, ,
, 。
。 为等差数列,并求数列
为等差数列,并求数列 项和为
项和为 ,令
,令 ,求
,求 的最小值。
的最小值。 成等差数列,
成等差数列, 成等比数列 ,则
成等比数列 ,则 等于( )
等于( ) 的前n项和为Sn,首项是
的前n项和为Sn,首项是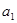 ,若
,若 Sn=
Sn= ,
, ,则公比
,则公比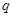 的取值范围是 .
的取值范围是 .