��Ŀ����
����Ŀ��ij��վ�����2014�귨���ڼ��յ��ݰ�����չ�����ʾ����飬�����A��B��C���ַżٷ��������������£�
֧��A���� | ֧��B���� | ֧��C���� | |
35������ | 200 | 400 | 800 |
35�����ϣ���35�꣩ | 100 | 100 | 400 |
��1�������в����������У��÷ֲ�����ķ�����ȡn���ˣ���֪����֧��A�����������г�ȡ��6�ˣ���n��ֵ��
��2������֧��B�����������У��÷ֲ�����ķ�����ȡ5�˿���һ�����壬����5��������ѡȡ2�ˣ���ǡ����1����35�����ϣ���35�꣩�ĸ���.
���𰸡���1��![]() ����2��
����2��![]() ��
��
��������
���⣨1���ֲ�������ǰ��������������ݴ���֧��A�����������г�ȡ������Ϊ6����ȷ��������Ϊ![]() ����n�ĵ�ֵΪ������������������
����n�ĵ�ֵΪ������������������![]() ����2����35�����µ�4�˱��Ϊ1,2,3,4����35�����ϵ�1�˱��Ϊa���г����еĻ����¼�����10�֣������¼���ǡ����1����35�����ϣ���35�꣩���������Ļ����¼�����������ŵ���͵ĸ��ʼ��㹫ʽ���ɣ�
����2����35�����µ�4�˱��Ϊ1,2,3,4����35�����ϵ�1�˱��Ϊa���г����еĻ����¼�����10�֣������¼���ǡ����1����35�����ϣ���35�꣩���������Ļ����¼�����������ŵ���͵ĸ��ʼ��㹫ʽ���ɣ�
��1�����ݷֲ������������ȡ������![]() �����
�����![]() ��
��
��2��35�����£�![]() ���ˣ�
���ˣ�
35�����ϣ�![]() ���ˣ�
���ˣ�
�裺��35�����µ�4�˱��Ϊ1,2,3,4����35�����ϵ�1�˱��Ϊa�����л����¼�Ϊ��
![]() ��10��.
��10��.
����������������![]() 4��.��
4��.��![]() .
.

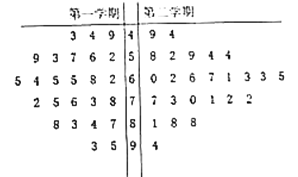
 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�