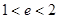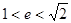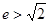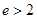题目内容
设 ,
, 分别为双曲线
分别为双曲线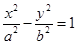
 的左,右焦点.若在双曲线右支上存在一点
的左,右焦点.若在双曲线右支上存在一点 ,满足
,满足 ,且
,且 到直线
到直线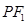 的距离等于双曲线的实轴长,则该双曲线的离心率为【 】.
的距离等于双曲线的实轴长,则该双曲线的离心率为【 】.
A. | B.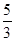 | C. | D. |
B
解析试题分析:利用题设条件和双曲线性质在三角形中寻找等量关系,得出a与b之间的等量关系,进而求出离心率.解:依题意|PF2|=|F1F2|,可知三角形PF2F1是一个等腰三角形,F2在直线PF1的投影是其中点,由勾股定理知,可知|PF1|=4b,根据双曲定义可知4b-2c=2a,整理得c=2b-a,代入c2=a2+b2整理得3b2-4ab=0,求得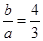 ,故可知双曲线的离心率为
,故可知双曲线的离心率为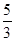 ,选B.
,选B.
考点:双曲线的性质
点评:解决的关键是根据双曲线于直线的位置关系,以及双曲线的几何性质来求解,属于中档题。

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
抛物线 的焦点坐标为( ) .
的焦点坐标为( ) .
A. | B. | C. | D. |
已知椭圆 上的一点
上的一点 到椭圆一个焦点的距离为
到椭圆一个焦点的距离为 ,则
,则 到另一焦点距离为
到另一焦点距离为
A. | B. | C. | D. |
过双曲线 的左焦点
的左焦点 作圆
作圆 的切线交双曲线右支于点
的切线交双曲线右支于点 ,切点为
,切点为 ,若
,若 ,则双曲线的离心率为
,则双曲线的离心率为
A. | B. | C. | D. |
已知椭圆 上的一点P,到椭圆一个焦点的距离为3,则P到另一焦点距离为( )
上的一点P,到椭圆一个焦点的距离为3,则P到另一焦点距离为( )
| A.2 | B.3 | C.5 | D.7 |
椭圆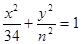 和双曲线
和双曲线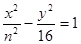 有相同的焦点,则实数
有相同的焦点,则实数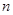 的值是 ( )
的值是 ( )
A.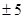 | B.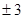 | C.5 | D.9 |
 的离心率为
的离心率为 .双曲线
.双曲线 的渐近线与椭圆
的渐近线与椭圆 有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆
有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆
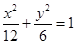


 的右顶点A作斜率为一1的直线,该直线与双曲线的两条渐近线的交点分别为B,C,若A,B,C三点的横坐标成等比数列,则双曲线的离心率为
的右顶点A作斜率为一1的直线,该直线与双曲线的两条渐近线的交点分别为B,C,若A,B,C三点的横坐标成等比数列,则双曲线的离心率为



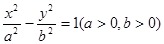 的右焦点F,作渐近线
的右焦点F,作渐近线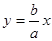 的垂线与双曲线左右两支都相交,则双曲线的离心率
的垂线与双曲线左右两支都相交,则双曲线的离心率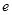 的取值范围为 ( )
的取值范围为 ( )