题目内容
已知函数f(x)=x3-3x2+2x
(1)在 处的切线平行于直线
处的切线平行于直线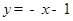 ,求
,求 点的坐标;
点的坐标;
(2)求过原点的切线方程.
(1)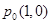 (2)y=-
(2)y=-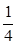 x.
x.
解析试题分析:(1)先求出函数的导函数,再求出函数在(2,-6)处的导数即斜率,易求切线方程.
(2)设切点为(x0,y0),则直线l的斜率为f'(x0)=3x02+1,从而求得直线l的方程,有条件直线1过原点可求解切点坐标,进而可得直线1的方程..
解:f′(x)=3x2-6x+2.
(1)设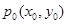 ,则
,则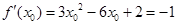 ,解得
,解得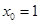 .则
.则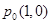
(2) ⅰ)当切点是原点时k=f′(0)=2,
所以所求曲线的切线方程为y=2x.
ⅱ)当切点不是原点时,设切点是(x0,y0),
则有y0=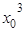 -3
-3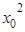 +2x0,k=f′(x0)=3
+2x0,k=f′(x0)=3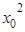 -6x0+2,①
-6x0+2,①
又k=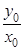 =
=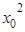 -3x0+2,②
-3x0+2,②
由①②得x0=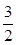 ,k=
,k=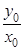 =-
=-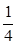 .
.
∴所求曲线的切线方程为y=-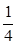 x.
x.
考点:直线的点斜式方程.

练习册系列答案
相关题目
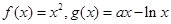 ,
, 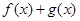 在
在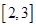 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;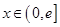 (
(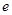 是自然常数)时,函数
是自然常数)时,函数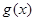 的最小值是3,若存在,求出
的最小值是3,若存在,求出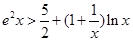 .
.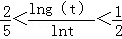 .
.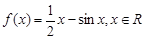 .
. 的递减区间;
的递减区间;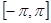 上的最值.
上的最值.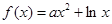 (
(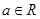 )
)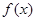 在区间[e,e2]上的最大值和最小值;
在区间[e,e2]上的最大值和最小值;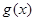 、
、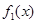 、
、 在公共定义域D上,满足
在公共定义域D上,满足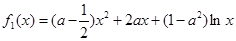 ,
,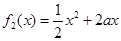 ,若在区间(1,+∞)上,函数
,若在区间(1,+∞)上,函数 ,曲线
,曲线 经过点
经过点 ,
, 处的切线为
处的切线为 .
. 、
、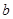 的值;
的值; ,使得
,使得 时,
时, 恒成立,求
恒成立,求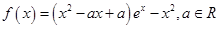 .
.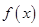 在
在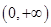 内单调递增,求
内单调递增,求 的取值范围;
的取值范围;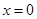 处取得极小值,求
处取得极小值,求 的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)
的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计) (弧度),将绿化带总长度表示为
(弧度),将绿化带总长度表示为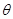 的函数
的函数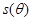 ;
;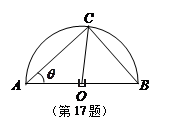
 的定义域是
的定义域是 ,其中常数
,其中常数 .(注:
.(注: 
 ,求
,求 的过原点的切线方程.
的过原点的切线方程. ,恒有
,恒有 .
. 时,求最大实数
时,求最大实数 ,使不等式
,使不等式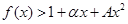 对
对 恒成立.
恒成立.