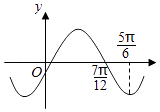题目内容
【题目】已知定义域为正整数集的函数f（x）=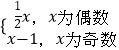 
，f1（x）=f（x），fn（x）=f[fn﹣1（x）]．若fn（21）=1，则n=；若f4（x）=1，则x所有的值构成的集合为 ．
【答案】6；{7，9，10，12，16}
【解析】解：∵定义域为正整数集的函数f（x）=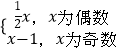 
，
f1（x）=f（x），fn（x）=f[fn﹣1（x）]．
fn（21）=1，
∴f6（21）=f5（20）=f4（10）=f3（5）=f2（4）=f1（2）=f（2）=1，
∴n=6．
∵f4（x）=1，
f4（16）=f3（8）=f2（4）=f1（2）=f（2）=1，
f4（12）=f3（6）=f2（3）=f1（2）=f（2）=1，
f4（10）=f3（5）=f2（4）=f1（2）=f（2）=1，
f4（9）=f3（8）=f2（4）=f1（2）=f（2）=1，
f4（7）=f3（6）=f2（3）=f1（2）=f（2）=1，
∴x所有的值构成的集合为{7，9，10，12，16}．
故答案为：6，{7，9，10，12，16}．
由f6（21）=f5（20）=f4（10）=f3（5）=f2（4）=f1（2）=f（2）=1，能求出n=6．由f4（x）=1，利用列举法能求出x所有的值构成的集合．
【题目】假设某种设备使用的年限x（年）与所支出的维修费用y（元）有以下统计资料：
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
参考数据： 
， 
，
如果由资料知y对x呈线性相关关系．试求：
（1）
；
（2）线性回归方程 
=bx+a．
（3）估计使用10年时，维修费用是多少？
【题目】某种商品价格与该商品日需求量之间的几组对照数据如表：
价格x（元/kg） | 10 | 15 | 20 | 25 | 30 |
日需求量y（kg） | 11 | 10 | 8 | 6 | 5 |
参考公式：线性回归方程 
，其中 
．
（1）求y关于x的线性回归方程；
（2）利用（1）中的回归方程，当价格x=40元/kg时，日需求量y的预测值为多少？