题目内容
9.已知集合A={x|1<x<m+3},集合B={x|m<x<m2+1}.(1)若m=3,求集合A∩B.
(2)若A?B,求实数m的取值范围.
分析 (1)当m=3时,可得A={x|1<x<6},B={x|3<x<10},利用交集的运算性质即可得出;
(2)若A?B,当A=φ时,则1≥m+3,即m≤-2.
若A≠φ,则$\left\{\begin{array}{l}m>-2\\ m≤1\\{m^2}+1≥m+3\end{array}\right.$,解出即可.
解答 解:(1)当m=3时,A={x|1<x<6},B={x|3<x<10},
故A∩B={x|3<x<6}.
(2)若A?B,当A=∅时,则1≥m+3,即m≤-2.
若A≠φ,则$\left\{\begin{array}{l}m>-2\\ m≤1\\{m^2}+1≥m+3\end{array}\right.$,
解得:-2<m≤-1,
综上:当m≤-1时,A?B.
点评 本题考查了分类讨论方法、集合的运算及其集合之间的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
4.已知集合M={x|0<x<3},N={x|log2x>1},则M∩N=( )
| A. | ∅ | B. | {x|0<x<3} | C. | {x|1<x<3} | D. | {x|2<x<3} |
14.若等差数列{an}的前三项和S3=15,则a2等于( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
19.有A、B、C、D、E共5人并排站一起,若A、B必须相邻,且B在A的右边,那么不同的站法有( )
| A. | 24种 | B. | 36种 | C. | 48种 | D. | 60种 |
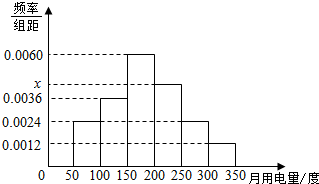 为调查我校学生的用电情况,学校后勤部门组织抽取了100间学生宿舍某月用电量调查,发现每间宿舍用电量都在50度到350度之间,其频率分布直方图如图所示.
为调查我校学生的用电情况,学校后勤部门组织抽取了100间学生宿舍某月用电量调查,发现每间宿舍用电量都在50度到350度之间,其频率分布直方图如图所示.