题目内容
已知圆 的圆心在
的圆心在 轴上,截直线
轴上,截直线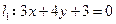 所得的弦长为
所得的弦长为 ,且与直线
,且与直线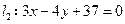 相切,求圆
相切,求圆 方程.
方程.
 的圆心在
的圆心在 轴上,截直线
轴上,截直线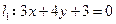 所得的弦长为
所得的弦长为 ,且与直线
,且与直线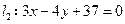 相切,求圆
相切,求圆 方程.
方程.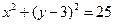
圆 的圆心在
的圆心在 轴上,所以设圆的方程为:
轴上,所以设圆的方程为: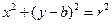 .
.
设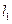 与圆
与圆 交于
交于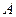 、
、 两点,则
两点,则 ,过
,过 作
作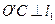 于
于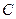 ,则
,则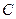 为弦
为弦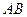 的中点,如图:
的中点,如图:
在 中,
中,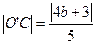 ,
, ,
,
所以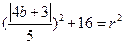 ①,
①,
又圆 与
与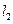 相切,则
相切,则 ②,
②,
将②代入①中得: .
.
解得: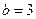 ;又代入②中,得
;又代入②中,得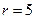 .
.
故圆 的方程为
的方程为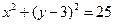 .
.
 的圆心在
的圆心在 轴上,所以设圆的方程为:
轴上,所以设圆的方程为: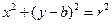 .
.设
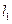 与圆
与圆 交于
交于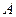 、
、 两点,则
两点,则 ,过
,过 作
作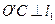 于
于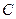 ,则
,则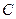 为弦
为弦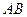 的中点,如图:
的中点,如图: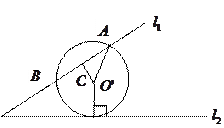 |
在
 中,
中,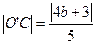 ,
, ,
,所以
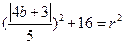 ①,
①,又圆
 与
与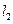 相切,则
相切,则 ②,
②,将②代入①中得:
 .
.解得:
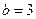 ;又代入②中,得
;又代入②中,得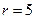 .
.故圆
 的方程为
的方程为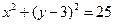 .
.
练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 的半圆上有两点
的半圆上有两点 ,设
,设 与
与 的交点是
的交点是 .
.

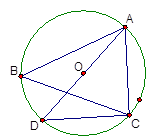
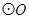 是
是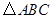 的外接圆,
的外接圆,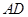 是
是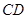 ,若
,若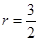 ,
,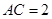 ,则
,则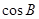 的值是( ).
的值是( ).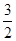
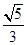
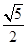

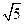 ,则这个圆的方程是___________.
,则这个圆的方程是___________.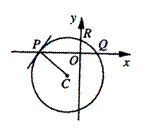
 的圆经过点
的圆经过点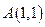 和
和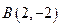 ,且圆心
,且圆心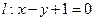 上,求圆心为
上,求圆心为 的圆心在直线
的圆心在直线 上,并且经过原点和
上,并且经过原点和 ,
, ,
, 两点,且截
两点,且截 轴所得的弦长为
轴所得的弦长为 .求此圆的方程.
.求此圆的方程.