题目内容
【题目】设函数f(x)=x2+bln(x+1),其中b≠0.
(1)当b=1时,求曲线y=f(x)在点(0,0)处的切线方程;
(2)讨论函数f(x)的单调性;
(3)当n∈N* , 且n≥2时证明不等式:ln[( ![]() +1)(
+1)( ![]() +1)…(
+1)…( ![]() +1)]+
+1)]+ ![]() +
+ ![]() +…+
+…+ ![]() >
> ![]() ﹣
﹣ ![]() .
.
【答案】
(1)解:f(x)=x2+ln(1+x),则f′(x)=2x+ ![]() ,
,
曲线y=f(x)在点(0,0)处的切线斜率为f′(0)=1,
切点为(0,0),则切线方程为y=x
(2)解:f′(x)=2x+ ![]() =
= 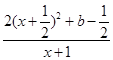 (x>﹣1),
(x>﹣1),
当b ![]() 时,f′(x)≥0,f(x)在x>﹣1上递增;
时,f′(x)≥0,f(x)在x>﹣1上递增;
当b< ![]() ,f′(x)=0,解得,x1=
,f′(x)=0,解得,x1= ![]() ,x2=
,x2= ![]() ,
,
①当b<0时,x1<﹣1,x2>﹣1,f′(x)>0,得x>x2,f′(x)<0,得﹣1<x<x2,
②当0<b< ![]() 时,x1>﹣1,x2>﹣1,f′(x)>0,得x>x2,﹣1<x<x1,f′(x)<0,得x1<x<x2;
时,x1>﹣1,x2>﹣1,f′(x)>0,得x>x2,﹣1<x<x1,f′(x)<0,得x1<x<x2;
综上可得,当b ![]() 时,f(x)的增区间为(﹣1,+∞);
时,f(x)的增区间为(﹣1,+∞);
当b<0时,f(x)的增区间为( ![]() ,+∞),减区间为(﹣1,
,+∞),减区间为(﹣1, ![]() );
);
当0<b< ![]() 时,f(x)的增区间为(
时,f(x)的增区间为( ![]() ,+∞),(﹣1,
,+∞),(﹣1, ![]() )
)
减区间为( ![]() ,
, ![]() )
)
(3)解:b=﹣1时,f(x)=x2﹣ln(x+1),
令h(x)=x3﹣f(x)=x3﹣x2+ln(x+1),h′(x)= ![]() 在x≥0恒正,
在x≥0恒正,
h(x)在[0,+∞)递增,x>0时,h(x)>h(0)=0,即当x>0时,x3﹣x2+ln(x+1)>0,
即ln(x+1)+x3>x2,对任意的n为正整数,取x= ![]() ,有ln(1+
,有ln(1+ ![]() )+
)+ ![]() >
> ![]() .
.
则ln[( ![]() +1)(
+1)( ![]() +1)…(
+1)…( ![]() +1)]+
+1)]+ ![]() +
+ ![]() +…+
+…+ ![]()
=ln(1+ ![]() )+ln(1+
)+ln(1+ ![]() )+…+ln(1+
)+…+ln(1+ ![]() )+
)+ ![]() +
+ ![]() +…+
+…+ ![]()
=ln(1+ ![]() )+
)+ ![]() +ln(1+
+ln(1+ ![]() )+
)+ ![]() +…+ln(1+
+…+ln(1+ ![]() )+
)+ ![]()
> ![]() +
+ ![]() +…+
+…+ ![]() >
> ![]() +
+ ![]() +…+
+…+ ![]()
= ![]() +
+ ![]() +…+
+…+ ![]()
= ![]() ﹣
﹣ ![]()
【解析】(1)求出导数,求出切线的斜率和切点,由点斜式的方程即可得到;(2)求出导数,讨论当b ![]() 时,当b<0时,0<b<
时,当b<0时,0<b< ![]() 时,令导数大于0得增区间,令导数小于0,得减区间,注意定义域;(3)b=﹣1时,f(x)=x2﹣ln(x+1),令h(x)=x3﹣f(x)=x3﹣x2+ln(x+1),求出导数,运用单调性得到当x>0时,x3﹣x2+ln(x+1)>0,即ln(x+1)+x3>x2,对任意的n为正整数,取x=
时,令导数大于0得增区间,令导数小于0,得减区间,注意定义域;(3)b=﹣1时,f(x)=x2﹣ln(x+1),令h(x)=x3﹣f(x)=x3﹣x2+ln(x+1),求出导数,运用单调性得到当x>0时,x3﹣x2+ln(x+1)>0,即ln(x+1)+x3>x2,对任意的n为正整数,取x= ![]() ,有ln(1+
,有ln(1+ ![]() )+
)+ ![]() >
> ![]() .再由对数的性质和裂项相消求和即可得证.
.再由对数的性质和裂项相消求和即可得证.
【考点精析】关于本题考查的利用导数研究函数的单调性和函数的最大(小)值与导数,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.
比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.

【题目】为了弘扬民族文化,某校举行了“我爱国学,传诵经典”考试,并从中随机抽取了100名考生的成绩(得分均为整数,满分100分)进行统计制表,其中成绩不低于80分的考生被评为优秀生,请根据频率分布表中所提供的数据,用频率估计概率,回答下列问题.
分组 | 频数 | 频率 |
[50,60) | 5 | 0.05 |
[60,70) | a | 0.20 |
[70,80) | 35 | b |
[80,90) | 25 | 0.25 |
[90,100) | 15 | 0.15 |
合计 | 100 | 1.00 |
(I)求a,b的值及随机抽取一考生恰为优秀生的概率;
(Ⅱ)按频率分布表中的成绩分组,采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;
(Ⅲ)在第(Ⅱ)问抽取的优秀生中指派2名学生担任负责人,求至少一人的成绩在[90,100]的概率.
【题目】随着智能手机的发展,微信越来越成为人们交流的一种方式.某机构对使用微信交流的态度进行调查,随机调查了 50 人,他们年龄的频数分布及对使用微信交流赞成人数如表.
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(I)由以上统计数据填写下面 2×2 列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若对年龄在[55,65),[65,75)的被调查人中随机抽取两人进行追踪调查,记选中的4人中赞成使用微信交流的人数为X,求随机变量X的分布列和数学期望
参考公式:K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
参考数据:
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |

