题目内容
某校高一学生1000人,每周一次同时在两个可容纳600人的会议室,开设“音乐欣赏”与“美术鉴赏”的校本课程.要求每个学生都参加,要求第一次听“音乐欣赏”课的人数为
 ,其余的人听“美术鉴赏”课;从第二次起,学生可从两个课中自由选择.据往届经验,凡是这一次选择“音乐欣赏”的学生,下一次会有20﹪改选“美术鉴赏”,而选“美术鉴赏”的学生,下次会有30﹪改选“音乐欣赏”,用
,其余的人听“美术鉴赏”课;从第二次起,学生可从两个课中自由选择.据往届经验,凡是这一次选择“音乐欣赏”的学生,下一次会有20﹪改选“美术鉴赏”,而选“美术鉴赏”的学生,下次会有30﹪改选“音乐欣赏”,用 分别表示在第
分别表示在第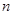 次选“音乐欣赏”课的人数和选“美术鉴赏”课的人数.
次选“音乐欣赏”课的人数和选“美术鉴赏”课的人数.
(1)若 ,分别求出第二次,第三次选“音乐欣赏”课的人数
,分别求出第二次,第三次选“音乐欣赏”课的人数 ;
;
(2)①证明数列 是等比数列,并用
是等比数列,并用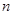 表示
表示 ;
;
②若要求前十次参加“音乐欣赏”课的学生的总人次不超过5800,求 的取值范围.
的取值范围.
(1)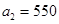 ,
,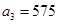 (2)①
(2)①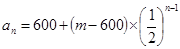 ②
②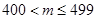 ,且
,且
解析试题分析:解决数列实际应用问题的关键是把实际问题随着正整数变化的量用数列表达出来,然后利用数列知识对表达的数列进行求解(求和、研究单调性、最值等),根据求解结果对实际问题作出答案.根据题意(1) ,分别取
,分别取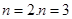 ,即可求出
,即可求出 ,(2)①由题意得
,(2)①由题意得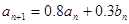 ,由
,由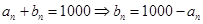 ,代入
,代入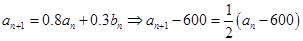 即可得证;②前十次听“音乐欣赏”课的学生总人次即为数列
即可得证;②前十次听“音乐欣赏”课的学生总人次即为数列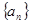 的前10项和
的前10项和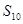 ,根据题意,
,根据题意,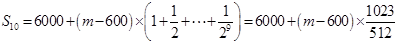 ,由已知,
,由已知,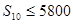 ,得
,得 ,解之即可.
,解之即可.
(1)由已知 ,又
,又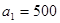 ,
,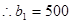 ,
,
∴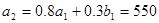 ,
,
∴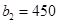 ,
,
∴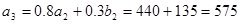 .
.
(2) ①由题意得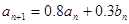 ,
,
∴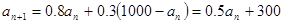 ,
,
∴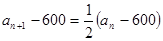 ,
, 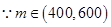 ,∴
,∴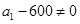 ,
,
∴数列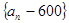 是等比数列,公比为
是等比数列,公比为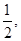 首项为
首项为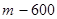
∴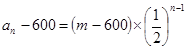 ,
,
得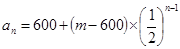
②前十次听“音乐欣赏”课的学生总人次即为数列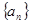 的前10项和
的前10项和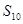 ,
,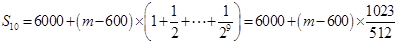 ,
,
由已知,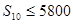 ,得
,得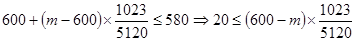 ,
,
∴ ,∴
,∴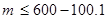 ,
,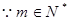 ,∴
,∴ 的取值范围是
的取值范围是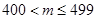 ,且
,且 .
.
考点:数列的实际应用问题

练习册系列答案
相关题目
 是等差数列,数列
是等差数列,数列 是等比数列,则
是等比数列,则 的值为 .
的值为 . 满足
满足 ,
, .
. ;
;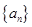 满足:
满足: .
.
 -100.
-100. 的首项
的首项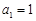 ,
, 是
是 项和,且
项和,且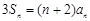
 .
.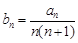 ,求数列
,求数列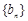 的通项公式;
的通项公式;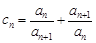 ,证明:
,证明: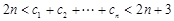 ,
,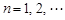 .
. 中各项均为正,有
中各项均为正,有 ,
, ,
, 中,
中, ,点
,点 在直线
在直线 上.
上. 和
和 的值;(2)求数列
的值;(2)求数列 和
和 ;
; ,求数列
,求数列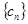 的前n项和
的前n项和 .
. 千元时多卖出
千元时多卖出 件。
件。 与n的函数关系式;
与n的函数关系式; 时,厂家应该生产多少件产品,做几千元的广告,才能获利最大?
时,厂家应该生产多少件产品,做几千元的广告,才能获利最大?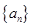 ,其前n项和
,其前n项和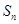 满足
满足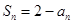 ;等差数列
;等差数列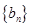 中
中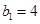 ,且
,且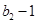 是
是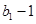 与
与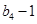 的等比中项
的等比中项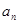 和
和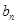 ,
,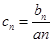 ,求
,求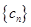 的前n项和
的前n项和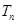 .
.