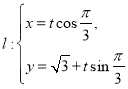Question

【题目】已知点M，N分别是椭圆C：（）的左顶点和上顶点，F为其右焦点，，椭圆的离心率为.

（Ⅰ）求椭圆C的方程；

（Ⅱ）设不过原点O的直线与椭圆C相交于A，B两点，若直线OA，AB，OB的斜率成等比数列，求面积的取值范围.

Answer 1

【答案】（Ⅰ）（Ⅱ）

【解析】

（Ⅰ）由，结合椭圆的离心率求解即可．

（Ⅱ）直线的斜率存在且不为0．设直线，，，，，联立直线和椭圆，消去可得，，利用判别式以及韦达定理，通过，，的斜率依次成等比数列，推出，求出，，且，然后求解三角形的面积的表达式，求解范围即可．

解：（Ⅰ）设椭圆的半焦距为，由题可知，，

，，则，

又，

解得，，，

所以椭圆C的方程

（Ⅱ）由题意可知，直线l的斜率存在且不为0.

故可设直线，，，

联立直线和椭圆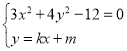，消去y可得，，

有题意可知，，

即，

且，，

又直线OA，AB，OB的斜率依次成等比数列，所以，

将，代入并整理得，

因为，，，且，

设d为点O到直线l的距离，则有，

，

所以，

所以面积的取值范围为