Question

【题目】如图所示，抛物线y=1﹣x2与x轴所围成的区域是一块等待开垦的土地，现计划在该区域内围出一块矩形地块ABCD作为工业用地，其中A、B在抛物线上，C、D在x轴上．已知工业用地每单位面积价值为3a元（a＞0），其它的三个边角地块每单位面积价值a元．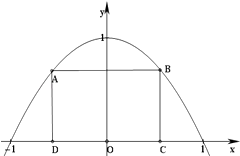

（1）求等待开垦土地的面积；
（2）如何确定点C的位置，才能使得整块土地总价值最大．

Answer 1

【答案】
（1）解：由 ，

故等待开垦土地的面积为

（2）解：设点C的坐标为（x，0），则点B（x，1﹣x2）其中0＜x＜1，

∴

∴土地总价值

=

由y′=4a（1﹣3x2）=0得

并且当 时，

故当 时，y取得最大值．

答：当点C的坐标为 时，整个地块的总价值最大．

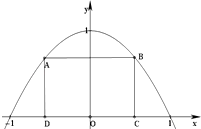
【解析】（1）先由定积分可求等待开垦土地的面积；（2）进而可得工业用地面积，三个边角地块面积，由此可得土地总价值，利用导数的方法可求函数的最值．