题目内容
【题目】已知函数f（x）= 
．
（1）判断f（x）在（0，+∞）的单调性；
（2）若x＞0，证明：（ex﹣1）ln（x+1）＞x2 ．
【答案】
（1）解：由函数f（x）的定义域为（﹣1，0）∪（0，+∞）
∴f′（x）= 
，
设g（x）= 
﹣ln（1+x），
∴g′（x）= 
﹣ 
= 
＜0，
∴g（x）在（0，+∞）为减函数，
∴g（x）＜g（0）=0，
∴f′（x）＜0，
∴f（x）在（0，+∞）为减函数
（2）解：（ex﹣1）ln（x+1）＞x2等价于 
＞ 
，
∵ = 
= 
，
∴原不等式等价于 ＞ ，
由（1）知，f（x）= 是（0，+∞）上的减函数，
∴要证原不等式成立，只需要证明当x＞0时，x＜ex﹣1，
令h（x）=ex﹣x﹣1，
∴h′（x）=ex﹣1＞0，
∴h（x）是（0，+∞）上的增函数，
∴h（x）＞h（0）=0，
即x＜ex﹣1，
∴f（x）＞f（ex﹣1），
即 ＞ =＞ ，
故（ex﹣1）ln（x+1）＞x2
【解析】（1）根据导数和函数单调性的关系，以及导数和最值得关系即可求出；（2）原不等式等价于 ＞ ，要证原不等式成立，只需要证明当x＞0时，x＜ex﹣1，令h（x）=ex﹣x﹣1，利用导数和最值得关系即可证明．
【考点精析】通过灵活运用利用导数研究函数的单调性，掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减即可以解答此题．
名校课堂系列答案
【题目】2017年年底，某商业集团根据相关评分标准，对所属20家商业连锁店进行了年度考核评估，并依据考核评估得分（最低分60分，最高分100分）将这些连锁店分别评定为A，B，C，D四个类型，其考核评估标准如下表：
评估得分 | [60,70） | [70,80） | [80,90） | [90,100] |
评分类型 | D | C | B | A |
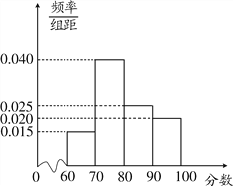考核评估后，对各连锁店的评估分数进行统计分析，得其频率分布直方图如下：
（Ⅰ）评分类型为A的商业连锁店有多少家；
（Ⅱ）现从评分类型为A，D的所有商业连锁店中随机抽取两家做分析，求这两家来自同一评分类型的概率．
