题目内容
(本小题满分14分)若函数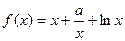 ,
,
(1)当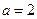 时,求函数
时,求函数 的单调增区间;
的单调增区间;
(2)函数 是否存在极值.
是否存在极值.
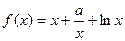 ,
,(1)当
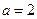 时,求函数
时,求函数 的单调增区间;
的单调增区间;(2)函数
 是否存在极值.
是否存在极值.解:(1)由题意,函数 的定义域为
的定义域为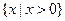 ………………2分
………………2分
当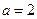 时,
时,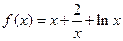 ,
,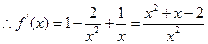 ……3分
……3分
令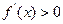 ,即
,即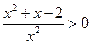 ,得
,得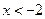 或
或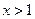 ………………5分
………………5分
又因为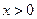 ,所以,函数
,所以,函数 的单调增区间为
的单调增区间为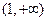 ………………6分
………………6分
(2)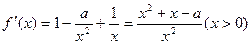 ……………7分
……………7分
解法一:令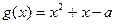 ,因为
,因为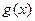 对称轴
对称轴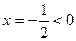 ,所以只需考虑
,所以只需考虑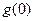 的正负,
的正负,
当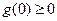 即
即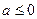 时,在(0,+∞)上
时,在(0,+∞)上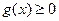 ,
,
即 在(0,+∞)单调递增,
在(0,+∞)单调递增, 无极值 ………………10分
无极值 ………………10分
当 即
即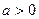 时,
时,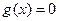 在(0,+∞)有解,所以函数
在(0,+∞)有解,所以函数 存在极值.…
存在极值.… 12分
12分
综上所述:当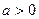 时,函数
时,函数 存在极值;当
存在极值;当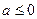 时,函数
时,函数 不存在极值.…14分
不存在极值.…14分
解法二:令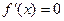 即
即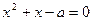 ,记
,记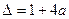
当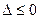 即
即
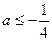 时,
时,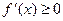 ,
, 在(0,+∞)单调递增,无极值 ………9分
在(0,+∞)单调递增,无极值 ………9分
当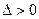 即
即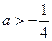 时,解
时,解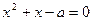 得:
得: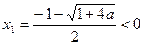 或
或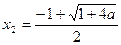
若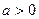 则
则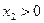 ,列表如下:
,列表如下:
由上表知: 时函数
时函数 取到极小值,即
取到极小值,即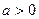 函数
函数 存在极小值。………11分
存在极小值。………11分
若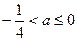 ,则
,则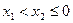 ,
, 在(0,+∞)单调递减,不存在极值。……13分
在(0,+∞)单调递减,不存在极值。……13分
综上所述,当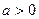 时,函数
时,函数 存在极值,当
存在极值,当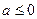 时。函数
时。函数 不存在极值……14分
不存在极值……14分
 的定义域为
的定义域为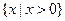 ………………2分
………………2分当
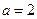 时,
时,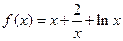 ,
,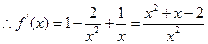 ……3分
……3分令
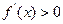 ,即
,即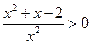 ,得
,得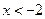 或
或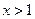 ………………5分
………………5分又因为
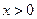 ,所以,函数
,所以,函数 的单调增区间为
的单调增区间为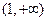 ………………6分
………………6分(2)
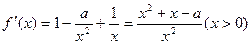 ……………7分
……………7分解法一:令
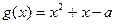 ,因为
,因为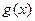 对称轴
对称轴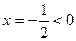 ,所以只需考虑
,所以只需考虑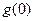 的正负,
的正负,当
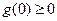 即
即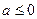 时,在(0,+∞)上
时,在(0,+∞)上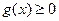 ,
,即
 在(0,+∞)单调递增,
在(0,+∞)单调递增, 无极值 ………………10分
无极值 ………………10分当
 即
即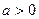 时,
时,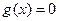 在(0,+∞)有解,所以函数
在(0,+∞)有解,所以函数 存在极值.…
存在极值.… 12分
12分综上所述:当
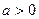 时,函数
时,函数 存在极值;当
存在极值;当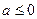 时,函数
时,函数 不存在极值.…14分
不存在极值.…14分解法二:令
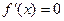 即
即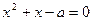 ,记
,记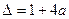
当
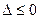 即
即
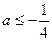 时,
时,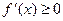 ,
, 在(0,+∞)单调递增,无极值 ………9分
在(0,+∞)单调递增,无极值 ………9分当
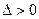 即
即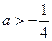 时,解
时,解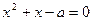 得:
得: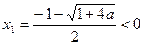 或
或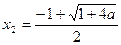
若
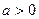 则
则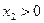 ,列表如下:
,列表如下: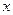 | (0, ) ) |  | ( ,+∞) ,+∞) |
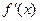 | — | 0 | + |
 | ↘ | 极小值 | ↗ |
 时函数
时函数 取到极小值,即
取到极小值,即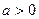 函数
函数 存在极小值。………11分
存在极小值。………11分若
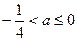 ,则
,则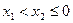 ,
, 在(0,+∞)单调递减,不存在极值。……13分
在(0,+∞)单调递减,不存在极值。……13分综上所述,当
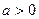 时,函数
时,函数 存在极值,当
存在极值,当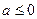 时。函数
时。函数 不存在极值……14分
不存在极值……14分略

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
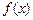 =
=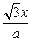 +
+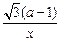 ,a≠0且a≠1.
,a≠0且a≠1.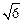 )上单调递减,在(
)上单调递减,在(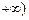 上单调递增,求a的值并写出函数的解析式;
上单调递增,求a的值并写出函数的解析式;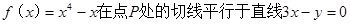 ,则点P的坐标为
,则点P的坐标为 )
) ,2)
,2)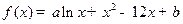 的一个极值点,(
的一个极值点,(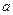 ,b∈R).
,b∈R).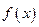 的单调区间;
的单调区间;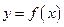 有3个不同的零点,求
有3个不同的零点,求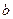 的取值范围.
的取值范围.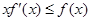 ,若
,若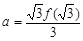 ,
,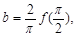
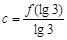 ,则
,则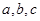 的大小关系是( )
的大小关系是( )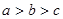
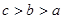
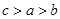
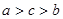
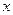 ,有
,有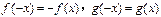 ,且
,且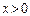 时,
时,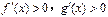 ,则
,则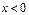 时 ( )
时 ( )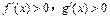
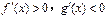
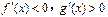
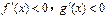
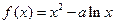 (常数
(常数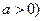 .
.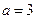 时,求曲线
时,求曲线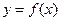 在点
在点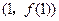 处的切线方程;
处的切线方程;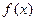 在区间
在区间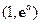 上零点的个数(
上零点的个数(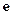 为自然对数的底数).
为自然对数的底数).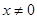 时,有不等式( )
时,有不等式( )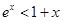
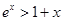
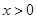 时
时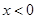 时
时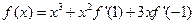 ,则
,则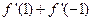 的值为___▲___.
的值为___▲___.